
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перевод чисел из одной системы счисления в другую
|
|
|
|
Теоретически возможно осуществить любой переход из  -ичной системы счисления в
-ичной системы счисления в  -ичную систему счисления. Однако при этом придется выполнять операции по правилам арифметики указанных не десятичных систем счисления. Поэтому более удобна форма перехода через промежуточную систему счисления, например, десятичную. Следовательно, необходимо рассмотреть два варианта:
-ичную систему счисления. Однако при этом придется выполнять операции по правилам арифметики указанных не десятичных систем счисления. Поэтому более удобна форма перехода через промежуточную систему счисления, например, десятичную. Следовательно, необходимо рассмотреть два варианта:
1. Перевод чисел из  -ичной системы счисления в десятичную.
-ичной системы счисления в десятичную.
2. Перевод чисел из десятичной системы счисления в  -ичную.
-ичную.
Перевод целой и дробной частей числа осуществляется по разному и результаты суммируется.
1. Перевод чисел из  -ичной системы в десятичную
-ичной системы в десятичную
Существует три варианта перевода: целой части числа  -ичной системы счисления в десятичную: по формулам степенного ряда, по схеме Горнера, по правилам перевода.
-ичной системы счисления в десятичную: по формулам степенного ряда, по схеме Горнера, по правилам перевода.
Алгоритм перевода по формулам степенного ряда:
1. Каждая цифра числа в  -ичной системе счисления переводится в число в десятичной системе счисления —
-ичной системе счисления переводится в число в десятичной системе счисления — 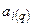 в
в  .
.
2. Полученные числа нумеруются в сокращенной записи справа налево, начиная с нуля — 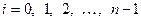 .
.
3. Десятичное число, соответствующее  -ой цифре исходного числа, умножается на
-ой цифре исходного числа, умножается на 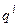 , где
, где  — номер цифры в исходном числе, и результаты произведений складываются.
— номер цифры в исходном числе, и результаты произведений складываются.
Все арифметические действия проводятся в десятичной системе счисления.
! Пример:. Перевод числа  в десятичную систему счисления по формулам стпенного ряда.
в десятичную систему счисления по формулам стпенного ряда.
1. 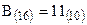 ,
, 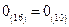 ,
, 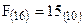 ,
, 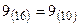 .
.
2. 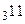 ,
,  ,
, 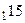 ,
,  .
.
3. 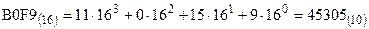
Чтобы избавиться от операции возведения в степень и минимизировать число арифметических операций при переводе применяется алгоритм Горнера (схема Горнера).
! Пример: Перевод 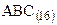 в десятичную систему счисления по схеме Горнера.
в десятичную систему счисления по схеме Горнера.
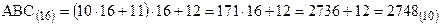 .
.
При переводе числа в двоичной системе счисления в десятичную систему необходимо в десятичной системе счисления сложить 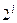 для тех разрядов двоичного числа, где содержатся 1.
для тех разрядов двоичного числа, где содержатся 1.
! Пример: 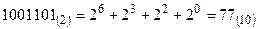 .
.
Перевод чисел в соответствии с правилами предполагает знание и использование правил выполнения арифметических операций в p-ичной системе счисления, что очень сложно. Поэтому данный способ рассматриваться не будет.
Перевода конечной  -ичной дроби в десятичную осуществляется по следующему алгоритму:
-ичной дроби в десятичную осуществляется по следующему алгоритму:
1. Целая часть числа переводится в десятичную систему отдельно.
2. Каждая цифра дробной части числа в  -ичной системе счисления переводится в число в десятичной системе.
-ичной системе счисления переводится в число в десятичной системе.
3. Полученные в результате преобразования дробной части числа нумеруются слева направо, начиная с единицы.
4. Десятичное число, соответствующее каждой  -ичной цифре, умножается на
-ичной цифре, умножается на  , где
, где 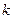 — номер этого числа, и результаты складываются, причем все эти арифметические действия проводятся в десятичной системе счисления.
— номер этого числа, и результаты складываются, причем все эти арифметические действия проводятся в десятичной системе счисления.
5. Результаты перевода целой и дробной части числа складываются.
! Пример: Перевод числа 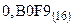 в десятичную систему счисления.
в десятичную систему счисления.
1.  .
.
2. 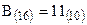 ,
, 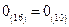 ,
, 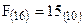 ,
, 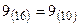 .
.
3. 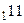 ,
,  ,
, 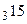 ,
, 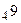 .
.
4. 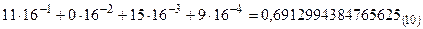 .
.
5. 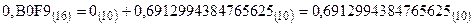 .
.
В данном случае также рекомендуется использовать схему Горнера, что минимизирует количество арифметических действий.
! Пример: 
2. Перевод числа из десятичной системы в  -ичную
-ичную
Алгоритм перевода целого числа из десятичной в  -ичную систему счисления (все вычисления выполняются в десятичной системе счисления):
-ичную систему счисления (все вычисления выполняются в десятичной системе счисления):
1. Делим исходное число 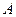 на
на  (основание новой системы счисления) нацело и записываем в качестве нового значения числа
(основание новой системы счисления) нацело и записываем в качестве нового значения числа 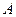 целую часть результата от деления.
целую часть результата от деления.
2. Остаток от деления образует соответствующую цифру в  -ичной системе счисления слева от полученных ранее цифр в
-ичной системе счисления слева от полученных ранее цифр в  -ичной записи числа
-ичной записи числа 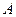 .
.
3. Выполняем пункты 1. и 2. до тех пор, пока число 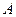 не станет равным нулю.
не станет равным нулю.
4. Выписываем ответ в виде полученных остатков в обратном порядке.
! Пример: Перевод числа 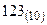 в троичную систему счисления.
в троичную систему счисления.
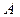 | Остаток
| Остаток
123 | 0
41 | 2
13 | 1
4 | 1
1 | 1
0 |
 .
.
Алгоритм перевода конечной десятичной дроби в  -ичную систему счисления:
-ичную систему счисления:
1. Умножаем дробную часть исходного числа 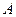 на
на  , целая часть полученного произведения является первой цифрой после запятой в искомом числе (целая часть может быть как равна нулю, так и быть больше девяти, но она всегда меньше
, целая часть полученного произведения является первой цифрой после запятой в искомом числе (целая часть может быть как равна нулю, так и быть больше девяти, но она всегда меньше  , что позволяет записать ее в виде одной цифры
, что позволяет записать ее в виде одной цифры  -ичной системы счисления).
-ичной системы счисления).
2. Дробную часть произведения снова умножаем на  , целую часть полученного числа заменяем на цифру в
, целую часть полученного числа заменяем на цифру в  -ичной системе счисления и приписываем ее справа к результату.
-ичной системе счисления и приписываем ее справа к результату.
3. Выполняем пункт 2. до тех пор, пока дробная часть произведения не станет равной нулю, или не выделится период.
! Пример: Перевод числа 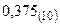 в двоичную систему счисления.
в двоичную систему счисления.
Дробная часть | Целая часть
0,375 | 0
0,75 | 1
0,5 | 1
0 |
 .
.
Десятичные дроби с конечным числом цифр при переводе в другие системы могут превратиться в бесконечные дроби. Если возможно найти период, то его следует выделить. Если же период выделить не представляется возможным, то определяется точность вычислений при переводе. Исходя из установленной точности производится округление после определенного числа знаков.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1627; Нарушение авторских прав?; Мы поможем в написании вашей работы!