Изоморфизм линейных пространств

Рассмотрим линейные пространства 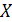и 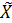пусть каждому элементу 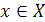поставлен в соответствие определенный элемент 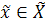, т. е. задана функция 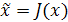, определенная всюду на 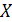, со значениями в 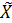. Будем говорить, что пространства 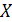и 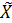(линейно) изоморфны, если найдется функция 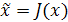, осуществляющая линейное и взаимно однозначное соответствие между 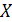и 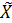, т. е.

1. 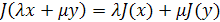для любых элементов 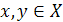и любых скаляров ;

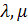2. если 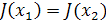, то ;

3. для любого 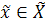найдется 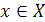такой, что .

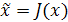Приведем примеры изоморфных линейных пространств.

Пример 1. Пространство многочленов с вещественными коэффициентами степени не выше 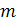изоморфно . Действительно, пусть

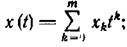
рассмотрим функцию 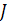, отображающую каждый такой многочлен в столбец 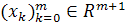, т. е.

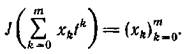
Упражнение. Проверьте, что 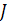— линейная, взаимно однозначная функция.

Пример 2. Всякое 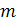-мерное вещественное линейное пространство 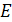изоморфно .

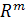Фиксируем в 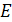базис . Тогда всякий 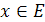однозначно представим в виде 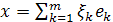. Положим для всякого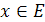

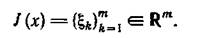
Если 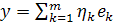, то т. е. справедливо свойство линейности координат: координаты линейной комбинации векторов равны той же линейной комбинации соответствующих координат этих векторов. Следовательно,

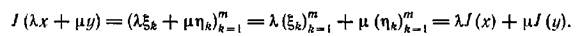
Взаимная однозначность 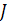есть следствие единственности координат вектора (при фиксированном базисе). Итак, 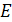изоморфно .

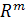Дата добавления: 2014-01-07