Введение. 1. Пусть — линейное пространство прямоугольных матриц порядка

Задачи

1. Пусть 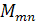— линейное пространство прямоугольных матриц порядка 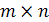. Докажите, что пространство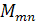 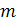-мерно. Найдите базис в 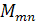в вещественном случае установите изоморфизм между 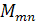и .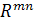

2. Покажите, что множество всевозможных дифференциальных операторов порядка не выше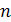

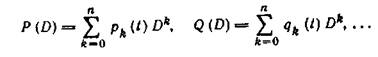
(здесь 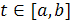коэффициенты 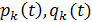непрерывны на 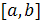, , 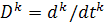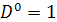) с операциями

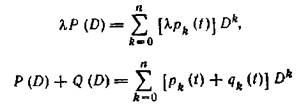
образует линейное пространство.

3. Во множестве 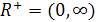положительных чисел (элементов) введем операции. Под «суммой» элементов 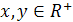будем понимать их произведение, а под «произведением» элемента 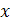на вещественное число 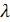будем понимать элемент 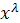Покажите, что при таком определении операций 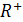превратилось в линейное пространство. Как выглядят в 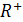«нуль» и «противоположный элемент»?

4. Докажите, что формула 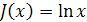, , 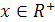осуществляет изоморфизм 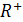на .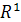

5 Обозначим через 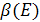множество всех подмножеств линейного пространства 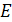. Если , то определим:

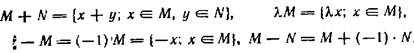
Какие из аксиом линейного пространства выполнены в ?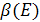

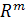
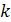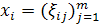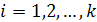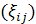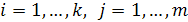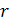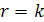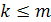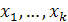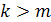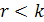6. Рассмотрим в столбцов , ; образуем из этих столбцов матрицу , пусть — ее ранг Покажите, что если и , то линейно независимы. Если же или , то 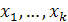линейно зависимы.

7. Докажите, что два конечномерных линейных пространства (оба веще­ственные или оба комплексные) изоморфны тогда и только тогда, когда их размерности совпадают.

8. Пусть 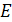и ‑ изоморфные конечномерные линейные пространства и формула 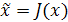осуществляет их изоморфизм. Докажите, что 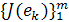— базис в , если — базис в .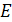

9. Пусть 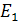и 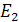— два линейных многообразия в линейном пространстве 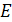Докажите формулу Грассмана 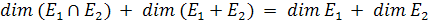- Здесь — размерность 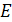, a 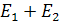— наименьшее линейное многообразие, содержащее 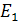и .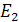

10. Пусть 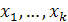— точки выпуклого множества 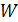в линейном пространстве 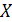, а 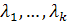, — неотрицательные скаляры такие, что 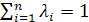. Тогда 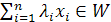. Докажите.

11. Пусть 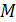и 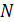выпуклы. Тогда множества 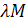и 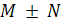(определение см. в задаче 5) также выпуклы. Докажите.

12.Пусть 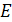— 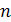-мерное вещественное пространство, а — комплексное пространство, полученное из 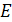после комплексификации. Какова размерность , если рассматривать его как вещественное пространство?

fffffffff

В предыдущей лекции мы рассмотрели линейные пространства. Следующим нашим шагом будет введение нормированных пространств. Понятие модуля вещественного числа, комплексного числа или вектора позволяет ввести расстояние, или, как принято говорить, метрику, на числовой оси, в комплексной плоскости или в пространстве векторов соответственно. Наличие метрики, в свою очередь, позволяет рассмотреть важнейшие вопросы о сходимости последовательностей и рядов, о предельном переходе, о непрерывности и дифференцируемости функций и т. п.

Дата добавления: 2014-01-07