Радиосигналы. Аналитическое, временное и спектральное представление радиосигналов

ЛЕКЦИЯ №2

Амплитудномодулированное колебание. Вид амплитудномодулированного колебания представлен на рис.2.4. Аналитическое выражение АМ-сигнала имеет вид:

,

где m - коэффициент модуляции. .

Рис.2.4 Спектральное (а) векторное (б) и временное представление АМ-сигнала

В случаях, когда требуются учитывать фазовые соотношения между составляющими спектра, удобно пользоваться векторным представлением АМ - сигнала (рис.2.4б), при этом рисунок должен вращаться синхронно с высокочастотной составляющей сигнала.

Эффективная ширина спектра АМ-сигнала:

1) Амлитудномодулированный сигнал DF = 2F_в,

где F_в - верхняя частота модуляции

2) Амплитудноманипулированный сигнал DF = 0, 8nN [Гц],

где n - номер верхней реализуемой гармоники (обычно n =3)

N - скорость телеграфирования в стандартных пятибуквенных словах в минуту N = 250 - 500 сл / мин.

В случае подавления одной боковой полосы ширина спектра уменьшается вдвое. При подавлении несущего колебания спектр:

DF = F_в - F_н, где F_н - нижняя частота модуляции.

Частотномодулированное колебание. На основе теории бесселевых функций уравнение описывающее ЧМ колебание:

,

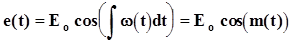примет вид ,

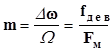- индекс модуляции.

Показать временное представление.

Рис.2.6 Частотномодулированное колебание

Дата добавления: 2014-01-07