Формула Ньютона-Лейбница

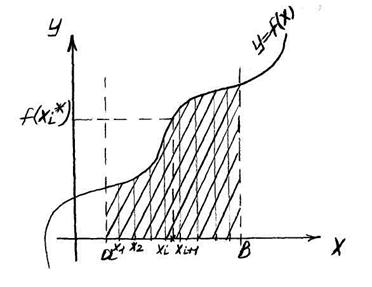
Задача о площади криволинейной трапеции. Понятие определенного интеграла.

Задача 1. Дана криволинейная трапеция, ограниченная прямыми 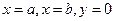и на .

Рассечем отрезок на части точками . В каждом из полученных частичных промежутков фиксируем точку .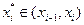

Т.к. 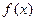непрерывна, а частичные промежутки малы, то можем считать, что функция мало меняется на каждом промежутке 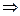площадь 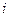-го столбика .Суммируя площади таких частичных промежутков .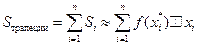

Переходя к пределу при максимальном из длин промежутков максималное 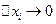, получим точное значение для площади трапеции (1).

Пусть на промежутке задана функция .

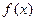Определение 1 Разбиением промежутка будем называть любой набор точек .

Определение 2 Если в каждом из частичных промежутков выбрана точка 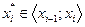, то говорят, что задано разбиение с фиксированными точками.

Возьмем некоторое разбиение 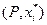промежутка и составим сумму .

Определение 3 Конечный предел называется определенным интегралом от функции 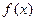по промежутку . Обозначается он , где 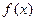- подынтегральная функция, - нижний и верхний пределы интегрирования.

Итак, непосредственно по определению, 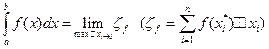(3)

Формула Ньютона-Лейбница

Определенный интеграл есть, как мы уже знаем, сумма большего числа бесконечно малых слагаемых, характеризующих элементарные площадки, под заданной функцией f(x).

Но вычислять его на практике, согласно, указанного определения, довольно сложно. Таким путем он не вычисляется. Для вычисления определенных интегралов, т. е. для определения площадей криволинейных фигур существует формула, являющаяся основной в интегральном исчислении и называется формулой Ньютона-Лейбница:

. (2-144)

Здесь f(x) - непрерывная на отрезке [a,b] функция; F(x)- любая ее первообразная, т. е. такая функция, что .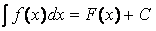

Формула Ньютона - Лейбница свидетельствует, что значение определенного интеграла 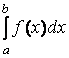связано со значением неопределенного интеграла Это связь совершенно неожиданна, т. к. по своему определению, и по своему смыслу определенный и неопределенный интеграл это совершенно разные вещи.

Для доказательства формулы Ньютона-Лейбница докажем первоначально лемму:

Доказательство.

Дадим некоторой, выбранной на отрезке [a,b], точке x приращение так, чтобы и . Тогда получаем

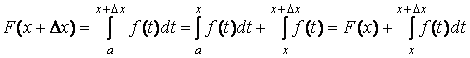
это, согласно свойства определенного интеграла. Отсюда следует:

.

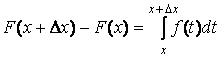Интеграл по теореме о среднем, равен

где .

Таким образом, откуда

Дата добавления: 2014-01-07