
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дебиеттер тізімі 5 страница
|
|
|
|
Қоректендіргіштердің активті және реактивті қуаттарының алгебралық қосындысының қосылғыштарының таңбасы токтың оң бағыты э.қ.к.-тің бағытымен сәйкес болған жағдайда плюс болады, егер, ал керісінше жағдайда минус болады. Қуаттар тепе-теңдігін комплекс түрде өрнектеуге болады: ∑ қор =∑
қор =∑ қаб, немесе ∑
қаб, немесе ∑ қор =∑ U қор Ỉқор = ∑Pқор +j∑Qқор, ∑
қор =∑ U қор Ỉқор = ∑Pқор +j∑Qқор, ∑ қаб =∑ U қаб Ỉқаб= ∑Pқаб +j∑Qқаб. Сондықтан ∑Pқор = ∑Pқаб, ∑Qқор = ∑Qқаб.
қаб =∑ U қаб Ỉқаб= ∑Pқаб +j∑Qқаб. Сондықтан ∑Pқор = ∑Pқаб, ∑Qқор = ∑Qқаб.
Топографиялық диаграммада оның белгілі бір нүктесіне тізбек сұлбасының белгілі бір нүктесінің комплекстік потенциалы сәйкес келеді. Потенциалы нөлге тең деп алынған сұлба нүктесі координаталар басына тура келеді. Топографиялық диаграмма тізбектің кез-келген нүктелерінің арасындағы кернеуді оңай анықтауға мүмкіндік береді. Ол үшін диаграммадағы тиісті нүктелерді түзумен қосады.
Негізгі әдебиеттер: [1(83-91, 97-102), 3(172-209)]
Қосымша әдебиеттер: [5,6,7,8]
Бақылау сұрақтары:
1.Синусоидалы токтың комплекстік мәндері үшін Ом және Кирхгоф заңдары.
2.Комплекстік кедергі. Комплекстік өткізгіштік.
3.Комплекстік қуат. Қуаттар тепе –теңдігі. Қуатты ваттметрмен өлшеу.
4. Топографиялық диаграммаға түсініктеме беріңіз.
№ 10 Дәріс.Екіұштылардың жиіліктік сипаттамалары. Кернеулер резонансы. Токтар резонансы
Екіұштық бір немесе бірнеше индуктивтіліктен және бір немесе бірнеше сыйымдылықтан тұрады делік. Мұндай екіұштықтың резонанстық режимі деп осы екіұштықтың кірістік кедергісі тек активті сипатта болып, реактивті кедергі немесе реактивті өткізгіштік нөлге тең болған жағдайды айтамыз. Басқаша айтқанда, сыртқы тізбекке қатысты екіұштық өзін резонанстық режимде активті кедергі секілді сезінеді. Сондықтан соның кірісіндегі кернеу және токтың фазалары бір-біріне сәйкес келеді. Ал екіұштықтың бұл кездегі реактивті қуаты нөлге тең болады. Резонанстық режимді екі түрге бөледі: кернеулер резонансы және токтар резонансы.
Электр тізбегінде кернеулер резонансы болу үшін мынадай екі шарт бір мезгілде орындалуы қажет: 1) r, L, C - элементтері тізбектей жалғануы керек; 2) индуктивті кедергі xL сыйымдылық кедергіге xC тең болу керек.
Резонанс кезінде:
а) Тізбектің толық кедергісі: , яғни толық кедергі, біріншіден, активті кедергіге тең болады, екіншіден, оның мәні минималды болады; ә) Тізбектегі ток: I= U/ z = U/ r, демек токтың мәні максималды болады; б) Фазалық ығысу:
, яғни толық кедергі, біріншіден, активті кедергіге тең болады, екіншіден, оның мәні минималды болады; ә) Тізбектегі ток: I= U/ z = U/ r, демек токтың мәні максималды болады; б) Фазалық ығысу:  , яғни қоректендіргіштің кернеуі мен токтың векторлары бір түзудің бойында жатады; в) Тізбектің элементтеріндегі кернеулер: Ua =Ir=(U/r)r=U, яғни активті кернеу толық кернеуге тең болады; индуктивті кернеу UL =IxL =(xL /r)U, сыйымдылық кернеу UC =IxC =(xC /r)U; xL =xC болғандықтан UL = UC,, демек, резонанс кезінде индуктивті кернеу сыйымдылық кернеуге тең болады, ал реактивті кернеу Up =UL - UC =0;
, яғни қоректендіргіштің кернеуі мен токтың векторлары бір түзудің бойында жатады; в) Тізбектің элементтеріндегі кернеулер: Ua =Ir=(U/r)r=U, яғни активті кернеу толық кернеуге тең болады; индуктивті кернеу UL =IxL =(xL /r)U, сыйымдылық кернеу UC =IxC =(xC /r)U; xL =xC болғандықтан UL = UC,, демек, резонанс кезінде индуктивті кернеу сыйымдылық кернеуге тең болады, ал реактивті кернеу Up =UL - UC =0;
Егер xL= xC >>r болса, онда UL = UC >U, яғни резонанс кезінде реактивті элементтердегі кернеу тізбекке берілген кернеуден бірнеше есе көп болуы мүмкін. Бұл апаттық жағдай тудыруы мүмкін.
 31-сурет
31-сурет
| г) Резонанс кезіндегі токтың және элементтердегі кернеулердің векторларың өзара орналасуы 31-суреттегі векторлық диаграммада көрсетілген; д) Резонанстық бұрыштық жиілік: ω0=1/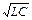 , резонанстық жиілік ƒ0=1/2π , резонанстық жиілік ƒ0=1/2π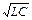 ; е) Сипаттамалық кедергі деп индуктивті кедергінің xL немесе сыйымдылық кедергінің xC резонанс кезіндегі мәнін айтады ; е) Сипаттамалық кедергі деп индуктивті кедергінің xL немесе сыйымдылық кедергінің xC резонанс кезіндегі мәнін айтады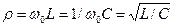
|
ж) Контурдың сапалылығы: 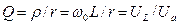 ; з) Өшу коэффициенті:
; з) Өшу коэффициенті:  , демек, ол сапалылыққа кері шама; и) Қуаттар: активті қуат P= I2r, индуктивті қуат QL= xLI2, сыйымдылық қуат QC= xCI2, реактивті қуат Qр= QL - QC=0, яғни резонанс кезінде реактивті қуат нөлге тең болады. Сонымен кернеулер резонансы кезінде ток максималды, ал xL= xC, UL= UC, QL= QC.
, демек, ол сапалылыққа кері шама; и) Қуаттар: активті қуат P= I2r, индуктивті қуат QL= xLI2, сыйымдылық қуат QC= xCI2, реактивті қуат Qр= QL - QC=0, яғни резонанс кезінде реактивті қуат нөлге тең болады. Сонымен кернеулер резонансы кезінде ток максималды, ал xL= xC, UL= UC, QL= QC.
r, L, C элементтері бірізді жалғанған тізбектің жиілік сипаттамалары. Мұндай тізбектегі ток:
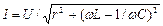 . Егер ω =0 немесе ω = ∞ болса, онда
. Егер ω =0 немесе ω = ∞ болса, онда  болады. Ал ω0 = 1/
болады. Ал ω0 = 1/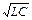 болса, онда ток I=U/ r максималды болады. Айталық, 0<ω<∞. Онда индуктивті кернеу:
болса, онда ток I=U/ r максималды болады. Айталық, 0<ω<∞. Онда индуктивті кернеу:  .
.
Егер  , онда
, онда  , ал егер
, ал егер онда
онда  .
.  -дің қандай жиілікте максималды болатындығын анықтау үшін бөлшектің бөлімін минимумға зерттейміз. Ол үшін бөлімнен бірінші ретті туынды алып, оны нөлге теңестіріп,
-дің қандай жиілікте максималды болатындығын анықтау үшін бөлшектің бөлімін минимумға зерттейміз. Ол үшін бөлімнен бірінші ретті туынды алып, оны нөлге теңестіріп,  -дің максималды болатын жиілігін табамыз:
-дің максималды болатын жиілігін табамыз:  >
> . Бұл жиілікте максималды мән
. Бұл жиілікте максималды мән  >UL0. UL0 – кернеу резонансы кезіндегі мәні.
>UL0. UL0 – кернеу резонансы кезіндегі мәні.
 Сыйымдылық элементтегі кернеу
Сыйымдылық элементтегі кернеу  .
.
Бұл өрнектің бөлімнен бірінші ретті туынды алып, оны нөлге теңестіріп, UC-дің максималды болатын жиілігін табамыз:  < ω0. Бұл жиілікте
< ω0. Бұл жиілікте  -дің максималды мәні
-дің максималды мәні 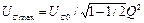 =ULmax. Егер
=ULmax. Егер  , онда
, онда  ,ал
,ал  болса, онда
болса, онда  .
.
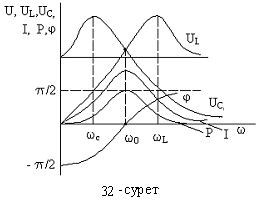
Сонымен UC максималды болатын жиілік ωС резонанстық жиіліктен ω0 кіші болады, ал  -дің максималды болатын жиілігі ωL резонанстық жиіліктен ω0 үлкен болады. Контурдың сапалылығы Q неғұрлым үлкен болған сайын, соғұрлым ωС пен ωL мәндері ω0-ден азырақ ауытқиды және резонанстық қисықтар тігірек, үшкірлеу болады (32- сурет).
-дің максималды болатын жиілігі ωL резонанстық жиіліктен ω0 үлкен болады. Контурдың сапалылығы Q неғұрлым үлкен болған сайын, соғұрлым ωС пен ωL мәндері ω0-ден азырақ ауытқиды және резонанстық қисықтар тігірек, үшкірлеу болады (32- сурет).
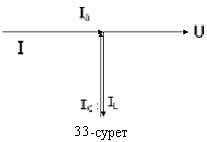 Токтар резонансы тізбекте мынадай шарттар бір мезгілде пайда болғанда болады: а) r, L, C элементтері параллель жалғануы керек (24-сурет); ә)сыйымдылық өткізгіштік bL индуктивті өткізгіштікке bC тең болуы керек, яғни bL=bC.
Токтар резонансы тізбекте мынадай шарттар бір мезгілде пайда болғанда болады: а) r, L, C элементтері параллель жалғануы керек (24-сурет); ә)сыйымдылық өткізгіштік bL индуктивті өткізгіштікке bC тең болуы керек, яғни bL=bC.
Резонанс кезінде:а) Тізбектің толық өткізгіштігі 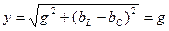 , яғни толық өткізгіштік минималды, ал толық кедергі максималды болады;
, яғни толық өткізгіштік минималды, ал толық кедергі максималды болады;
ә) Тізбектің толық тогы  =Ug, демек ток минималды болады.
=Ug, демек ток минималды болады.
 б) Фазалық ығысу
б) Фазалық ығысу  ;
;
в) Тізбектің тармақтарындағы токтар: Ia= Ug, IL=UbL,, IC=UbC, яғни IL= IC,. Реактивті ток Iр=IL-IC=0. Ал I=Uy=Ug=Ia, демек,толық ток активті токқа тең. г) 33-суреттегі диаграммада резонанс кезіндегі токтардың векторларының өзара орналысуы көрсетілген; д) резонанстық жиілік ƒ0=1/2π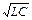 ; е) Қуаттар: активті қуат P= U2g, индуктивті қуат QL= U2bL, сыйымдылық қуат QC= U2bC, демек QL= QC; Реактивті қуат Qp= QL - QC= 0;
; е) Қуаттар: активті қуат P= U2g, индуктивті қуат QL= U2bL, сыйымдылық қуат QC= U2bC, демек QL= QC; Реактивті қуат Qp= QL - QC= 0;
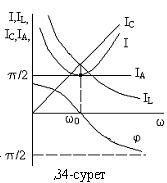
34-суретте параллель контурдың жиіліктік сипаттамасының қисықтары көрсетілген. Сыйымдылық элементтегі ток IC =ωCU жиілікке пропорционал өседі, ал индуктивті элементтегі ток IL=U/ωL жиілікке кері пропорционал өзгереді. Резистивті элементтегі ток Ir=U/r жиілікке тәуелді емес. IC мен IL қисықтарының қиылысқан нүктесі токтар резонансына сәйкес келеді. Бұл жағдайда I=Ir.
Реалды жағдайда 24-суреттегі индуктивті элемент пен активті кедергі r2, ал сыйымдылық элемент пен активті кедергі r3 бірізді жалғануы мүмкін. Бұл кедергілер арқылы сымдардағы энергия шығыны есепке алынады. Мұндай тізбекте токтар резонансы болу шарты: bL=bC, 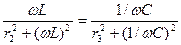 , бұдан резонанстық бұрыштық жиілік
, бұдан резонанстық бұрыштық жиілік 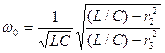 .
.
Бұл жағдайда да резонанс кезінде толық ток пен кернеумен фаза бойынша сәйкес келеді.
Негізгі әдебиеттер: [1(113-123, 97-102), 2(223-234)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1.Екіұштықтың резонанстық режим кезіндегі жұмыстарына тоқталыңыз. Резонанстық режим деген қандай режим және оның қандай түрлері бар?
2. Активті және реактивті элементтерді тізбектей қосқанда байқалатын кернеулер резонансына түсініктеме беріңіз. Кернеулер резонансы кезінде тізбекті сипаттайтын электрлік параметрлердің мәндері мен сипаттары қандай өзгеріске түседі?
3. Токтар резонансына түсініктеме беріңіз. Резонансы кезіндегі тізбектің толық өткізгіштігін, тізбек тармақтарындағы токтарды және фазалық ығысуды сипаттаңыз.
4.Резонанстық жиіліктік сипаттамаға түсініктеме беріңіз.
№11 Дәріс. Индуктивті байланысқан элементтері бар тізбектер
Тізбектің бір контурында немесе бір элементінде ток өзгерген кезде басқа контурда немесе басқа элементте э.қ.к. пайда болса, онда осы екі контурды немесе екі элементті бір-бірімен индуктивті байланысқан (магнитті байланысқан) дейді, ал екінші контурда немесе екінші элементте пайда болған э.қ.к.-ті өзаралық индукцияның э.қ.к.-і деп атайды.
Өзара қатар ораласқан, орам сандардары w1 және w2 тең екі индуктивтілік орамалармен i 1 және i 2 токтары жүрсе, онда әр ораманың барлық магнит сызықтары екінші ораманың орамдарымен ілінісуі мүмкін, яғни Ф21 =Ф11, Ф12 =Ф22. Сондықтан мұндай тізбектерді талдау кезінде орамалардың өздерінің ағын ілінісулерінен (Ψ11 және Ψ22) басқа қосымша ағын ілінісулерін (Ψ12 және Ψ21) есепке алу керек. Бірінші ораманың өзіндік ағын ілінісуі Ψ11=Ф11 w1= L1 i 1, бірінші ораманың тогының әсерінен пайда болған екінші орамадағы қосымша ағын ілінісуі Ψ21= Ф21 w2 =Ф11 w2=М21 i 1, мұндағы М21= Ψ21/ i 1 –пропорциональдық коэффициент, өзаралық индуктивтілік деп аталады. Бұл өрнектерден
L1/ М21= w1/ w2.
Екінші ораманың өзіндік ағын ілінісуі Ψ22=Ф22 w2= L2 i 2, екінші ораманың тогының әсерінен пайда болған бірінші орамадағы қосымша ағын ілінісуі Ψ12= Ф12 w1 =Ф22 w1=М12 i 2. Бұл өрнектерден L2/ М12= w2/ w1. Көрсетілген екі қатынастан М12 М21= L1L2 екендігін көруге болады. Тәжірибе М12 = М21=М екендігін көрсетеді. Демек, өзаралықиндуктивтілік М= .
.
Егер бір ораманың магнит сызықтарының тек біраз бөлігі ғана екінші орамамен ілініссе, яғни Ф21 <Ф11, Ф12 <Ф22 болса, онда өзаралықиндуктивтілік М=К , мұндағы К= М /
, мұндағы К= М / - байланыс коэффиценті деп аталады. Бұл коэффициенттің мәні бірден кіші К <1, өйткені Ф21 <Ф11, Ф12 <Ф22, яғни бір ораманың магнит ағыны екінші ораманы толық қамтымайды.
- байланыс коэффиценті деп аталады. Бұл коэффициенттің мәні бірден кіші К <1, өйткені Ф21 <Ф11, Ф12 <Ф22, яғни бір ораманың магнит ағыны екінші ораманы толық қамтымайды.
Өзаралықиндуктивтілік токтардың мәндері мен бағыттарына тәуелді емес, ол орамалардың құрылысымен және өзара орналасуымен анықталады. Қарастырылған екі ораманың толық ағын ілінісуі Ψ екі құраушыдан тұрады. Құраушылар токтардың бағыттарына және өзара орналасуына байланысты қосылуы немесе бірі бірінен алынуы мүмкін. Сұлбада орамалардың аттас ұштарын (қысқыштарын) нүктелер арқылы белгілейді (35-сурет). Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болса, онда орамалар өзара үйлесімді қосылған (35а-сурет). Бұл жағдайда бірінші ораманың толық ағын ілінісуіΨ1 = Ψ11+ Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2 = Ψ22+ Ψ21.Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған (35ә-сурет). Бұл кезде бірінші ораманың толық ағын ілінісуі Ψ1 = Ψ11 - Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2 = Ψ22 - Ψ21.
Өзаралық индукцияның э.қ.к.-і. Егер өзаралық ағын ілінісуі уақытқа тәуелді өзгерсе, онда орамаларда өзаралық индукцияның э.қ.к.-тері пайда болады: е2м= -d Ψ21 /dt, немесе е2м= -Mdi 1/dt, ал бірінші орамада е 1м = -d Ψ12 /dt, немесе е 1м =- Mdi 2/dt. Екінші орамада пайда болған өзіндік индукция э.қ.к.-і бірінші орамадағы токтың өзгерісіне қарсы әсер етеді.
  а) б)
35-сурет
а) б)
35-сурет
 а) а)
 ә) ә)
 б)
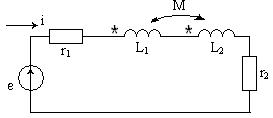
36-сурет
б)
36-сурет
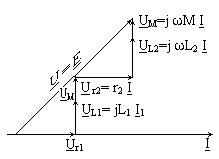
| Индуктивті байланысқан элементтер бірізді жалғанған тізбек(36а-сурет).Тізбек бірізді қосылған r1 мен r2 активті кедергілерден және L1 мен L2 индуктивтіліктен құралсын. Индуктивті элементтер арасындағы магниттік байланысты өзара индуктивтілік М сипаттайды. Оларды тізбекке қосудың екі сұлбасы болуы мүмкін. Индуктивтілік орамаларды үйлесімді қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток бір бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары қосылады. 36а–суретте көрсетілген тізбек үшін Кирхгоф екінші заңы бойынша теңдеу құрайық. Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған. Бұл жағдайда бірінші ораманың толық ағын ілінісуі Ψ1 = Ψ11 - Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2 = Ψ22 - Ψ21. Ir 1+ L 1 di/dt + M di/dt+L 2 di/dt+ M di/dt+ir 2 = e. Комплекстік түрде: I[ r 1+ r 2+ jω(L1+L2+2M)]= E. Бұдан орамалар үйлесімді қосылған кездегі олардың толық индуктивтілігін анықтаймыз: Lүйл =L1+L2+2M. Тізбектің толық кедергісі Z үйл=r 1+ r 2+ jω(L1+L2+2M)= Z 1+ Z 2+2 Z m, мұндағы Z 1=r1+ jωL1, Z 2= r 2+ jωL2,, Z m= jωM.- орамалардың комплекстік кедергілері және өзара индукцияның комплекстік кедергісі. Орамалар үйлесімді қосылған жағдайға сәйкес келетін векторлық диаграма 36ә–суретте көрсетілген. Орамаларды қарсы қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток қарама-қарсы бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары бір-біріне қарсы бағытталады, яғни толық магнит ағыны азаяды. Бұл жағдайда Кирхгофтың екінші заңы |
бойынша құрылған теңдеу:
Ir 1+ L 1 di/dt - M di/dt+L 2 di/dt- M di/dt+ir 2 = e.
Комплекстік түрде: I[ r 1+ r 2+ jω(L1+L2 -2M)]= E
Орамалар қарсы қосылған кездегі олардың толық индуктивтілігін анықтаймыз: Lқар =L1+L2 -2M. Тізбектің толық кедергісі Z қар= r 1+ r 2+ jω(L1+L2 -2M)= Z 1+ Z 2 - 2 Z m,
36б -суретте орамалардың қарсы қосылған сұлбасына сәйкес келетін векторлық диаграмма көрсетілген.
Индуктивті байланысқан элементтер параллель жалғанған тізбек. Өзара индуктивтігі М, кедергілері r1 мен r2, ал индуктивтері L1 мен L2 болатын екі қабылдағыш параллель қосылған.
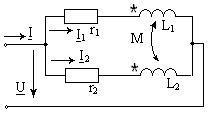 37-сурет
37-сурет
| Орамалардың аттас ұштары бір түйінге қосылған (37 -сурет). Токтар мен кернеулердің таңдап алынған оң бағытында I = I 1 + I 2; U = Z 1 I 1+ Z m I 2; U = Z m I 1+ Z 2 I 2,,мұндағы Z 1=r1+ jωL1,, Z 2=r 2+ jωL2,, Z m=jωM. Бұл теңдеулерді шешкенде  ; ; ; ; ; ;
|
Бұдан тізбектің комплекстік кедергісі 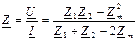 .
.
Тізбектің толық индуктивтігі Lүйл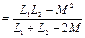 . Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z m=0 болғанда, бұл өрнек мына түрге келеді:
. Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z m=0 болғанда, бұл өрнек мына түрге келеді:  .
.
Егер орамалардың аттас ұштары әр түйінге қосылған болса, яғни орамалар қарсы қосылған жағдайда, кернеудің теңдеуіндегі Z m таңбасы минусқа өзгереді. Демек, бұл жағдайда тізбектің кірістік комплекстік кедергісі  , ал толық индуктивтілігі Lқар
, ал толық индуктивтілігі Lқар 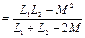 .
.
Индуктивті байланысқан элементтер бар күрделі тізбекті есептеу. Мұндай тізбектерді есептеу үшін Кирхгоф екінші заңы бойынша теңдеулер құрған кезде, индуктивті орамалар үшін жазылатын кернеулердің өрнегіне өзара индукцияның комплекстік кернеуін  jωM I қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.
jωM I қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.
Индуктивті байланысқан элементтері бар тізбекті индуктивті байланысы жоқ балама сұлбамен ауыстыру арқылы тізбекті есептеуді жеңілдетуге болады. Екі элементтен (Z 1 және Z 2) тұратын индуктивті байланысы бар тізбекті балама сұлбамен ауыстырғанда Z 1 мен Z 2 кедергілеріне  Z м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына
Z м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына  Z м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса, онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.
Z м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса, онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.
Темір өзекшесіз трансформатор (ауа трансформаторы). Трансформатор деп тізбектегі энергияны басқа тізбекке электромагниттік индукция құбылысы арқылы беретін аппаратты айтады.
Оның қарапайым түрі ферромагниттік өзекшесіз индуктивті байланысқан екі орамадан тұрады. Кернеу көзі бірінші орамаға қосылады, ал жүктеме екінші орамаға қосылған.
Трансформатордың теңдеулері мына түрде жазылады:
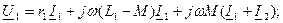
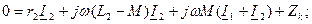
Мұндағы r1, L1 және r2 , L2 – бірінші және екінші орамалардың активті кедергілері және индуктивтері; Z қ = rқ +jXқ –жүктеменің кедергісі; I 1, I 2 – бірінші және екінші орамадағы токтар.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1043; Нарушение авторских прав?; Мы поможем в написании вашей работы!