Дебиеттер тізімі 6 страница

Екінші орамадағы ток: I₂ =-jX_m I ₁ /(r_2қ +jX_2қ). Токты трансформациялау коэффициенті: k_i=I₂ /I₁ =X_m /z_2қ. Кернеуді трансформациялау коэффициенті: k_u = U₂ / U₁. Егер L₁ < M<L₂ болса,онда L₁ - M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ > U₁, демек, трансформатор кернеуді жоғарлатады. Егер L₁ > M > L₂ болса,онда L₂ - M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ <U₁, демек, трансформатор кернеуді төмендетеді.

Негізгі әдебиеттер: [1(124-144), 3(278-302)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Тізбектің индуктивті байланыстағы элементтері жөнінде түсініктеме беріңіз. Байланыс коэффициенті қалай анықталады?

2. Өзара индукцияның э.қ.к.-і дегеніміз не? Орамалардың өзара үйлесімді және қарсы қосылуы туралы түсініктеме беріңіз.

3. Индуктивті байланысқан элементтері бірізді жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

4. Индуктивті байланысқан элементтері параллель жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

5.Темір өзекшесіз трансформатор (ауа трансформаторы туралы түсініктеме беріңіз.

№12 Дәріс. Үш фазалы қоректендіргіштер және үш фазалы тізбектер туралы түсініктемелер. Қоректендіргіш пен қабылдағыштың фазалары жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбек

Электр тізбегінің көп фазалы жүйесі деп жиіліктері бірдей, ал фаза бойынша бірі бірінен ығысқан бірнеше айнымалы э.қ.к-тер тізбектерінің жиынтығын айтады. Көбінесе практикада амплитудалары тең және фазалары бойынша 2π/ т – бұрышқа ығысқан (мұндағы т- фаза саны) бірнеше э.қ.к.-терден тұратын көп фазалық симметриялық жүйелер қолданылады. Қазіргі кезде көп фазалық жүйелердің ішінде ең көп тарағаны -үш фазалы жүйелер.

Үш фазалы симметриялы э.қ.к.-тер жүйесі деп бірдей жиілікті және бірдей амплитудалы, ал фаза бойынша 120⁰ ығысқан үш синусоидалы э.қ.к.-тердің жиынтығын айтады.

Үш фазалы симметриялы э.қ.к.-тер жүйесін алу үшін үш фазалы синхронды генератор қолданылады. Оның статорында бірі бірінен 120⁰-қа ығысқан және өзара оқшауланған үш фазалық орама орналасқан. Ротор айналғанда осы орамаларда амплитудалары бірдей, жиіліктері бірдей, бірақ фаза бойынша 120⁰- қа ығысқан үш э.қ.к.-тер пайда болады. Олардың біреуін е _А (Е _А ), одан фаза бойынша 120⁰ кеш қалған екіншісін е_В (Е _В), ал біріншіден фаза бойынша 120⁰ озған э.қ.к.-і е_С (Е _С) белгілейміз.

Генератордың орамаларын оның фазалары деп атайды да, А,В,С латын әріптері арқылы белгілейді. Фазалар кезектесуі деп э.қ.к.-тердің белгілі бір мәнге ие болу кезіндегі ретін айтады. Егер бұл рет Е _А, Е _В, Е _С болса, онда мұндай кезектесу тура кезектесу деп аталады.

Симметриялы генератордың фазалық орамаларының э.қ.к.-тердің лездік мәндері:

е _А =Е _тsinωt, е_В =E_msin(ωt- 120⁰), е_С=E_msin(ωt+ 120⁰).

Э.қ.к.-тердің комплекстік әрекеттік мәндері: Е _А =Е_фе^j0˚, E _B= Е_фе ^-j120˚, E _C= Е_фе ^j120˚.

Э.қ.к.-тердің комплекстік әрекеттік мәндерінің алгебралық қосындысы нөлге тең және э.қ.к.-тердің лездік мәндерінің алгебралық қосындысы да нөлге тең: Е _А+ E _B+ E _C=0; е _А+ е_В+ е_С =0.

Үш фазалы тізбек деп үш фазалы э.қ.к.-тер жүйесі мен үш фазалы қабылдағыштың (жүктеменің) және жалғау сымдарының жиынтығын айтады. Үш фазалы тізбектің фазасы деп оның бойымен белгілі бір ток ғана жүретін бөлігін айтады. Үш фазалы жүйе алу үшін генератордың мен жүктеменің фазаларын өзара әр түрлі сұлба бойынша қосады:

1.Алты сым арқылы жалғану сұлбасы (38-сурет). А, В,С- генератор орамаларының басқы ұштары; x,y,z- орамалардың аяққы ұштары;

Бұл сұлба бойынша генератордың әр фазасы жүктеменің әр фазасымен екі сым арқылы жалғанады. Барлығы алты сым керек болады.. Бұл сұлба экономикалық жағынан тиімсіз.

2. Жұлдызша сұлба бойынша жалғағанда ораманың аяққы ұштары x,y,z бір нүктеге (түйінге) қосылады және ол нүктені үш фазалы қоректендіргіштің нөлдік нүктесі немесе бейтарап нүктесі (О) деп атаймыз(39а-сурет). Сол сияқты жүктеменің де фазаларының бір ұштары бір нүктеге (түйінге) қосылады және ол нүктені жүктеменің нөлдік нүктесі немесе бейтарап нүктесі (О′) деп атаймыз. Генератордың орамаларының басқы ұштарын жүктемемен қосатын сымдарды желілік сымдар деп атайды, ал олар арқылы жүретін токтар желілік токтар I _A, I _B, I _C деп аталады. Бұл токтар генератордан жүктемеге қарай бағытталған. Генератордың бейтарап нүктесін жүктеменің бейтарап нүктесімен жалғайтын сымды нөлдік немесе бейтарап сым деп аталады. Бейтарап сыммен жүретін ток нөлдік ток (I ₀) немесе бейтарап ток деп аталады және ол жүктемеден генераторға карай бағытталады.

Үш фазалық жүйеде генератордың фазалық орамаларының ұштарының арасындағы немесе жүктеменің фазаларының ұштарының арасындағы кернеулерді (U _A, U _B, U _C ) ф азалық кернеулер деп аталады. Бұл кернеулерді желілік сымдар мен нөлдік сым арасындағы кернеулер деп де қарастыруға болады. Симметриялы жүйеде фазалық кернеулердің әрекеттік мәндері бірдей болады: U_A =U_B=U_C = U_ф.

Фазалық токтар деп генератордың фазалық орамалары немесе жүктеменің фазалары арқылы жүретін токты айтады.

Желілік кернеулер (U _AB, U _BC, U _CA ) деп желілік сымдар арасындағы кернеулерді айтамыз. Желілік кернеулерді фазалардың бастапқы ұштарының арасындағы кернеулер деп де қарастыруға болады. Симметриялы жүйеде желілік кернеулердің әрекеттік мәндері бірдей болады: U_AB = U_BC = U_CA = U_ж.

Егер U _A = Е _А, U _B = E _B, U _C = E _C ескерсек, онда желілік кернеулердің комплекстік мәндері: U _AB = Е _А - E _B = U _A - U _B = U_ж e^j30˚, U _BC= E _B- E _C= U _B- U _C = U_ж e ^–j90˚ , U _CA= E _C- E _A= U _C- U _A = U_ж e ^j150˚.

Үш фазалы симметриялы қоректендіргіштің фазалары жұлдызша жалғанған кезде фазалық және желілік кернеулер үшін векторлық диаграмма 39ә – суретте көрсетілген. Бұл диаграммадан фазалық және желілік кернеулердің комплекстік мәндері үш бірдей теңбүйірлі үшбұрыш құрайтындығын көреміз. Бұл үшбұрыштан желілік және фазалық кернеулердің әрекеттік мәндері өзара мынадай қатынаста болатындығын көреміз: U_ж =2U_Фcos30˚= .

Қоректендіргіш пен қабылдағыштың (жүктеменің) фазаларының токтары: I = E_A / Z _A = U _A/ Z _A, I _B= E _B/ Z _B= U _B/ Z _B, I _C= E _C/ Z _C= U _C/ Z _C. Бейтарап сымдағы ток I ₀ = I _A + I _B + I _C. Қоректендіргіш пен қабылдағыштың (жүктеменің) фазалары жұлдызша сұлба бойынша жалғанса, желілік токтар оларға сәйкес фазалық токтарға тең болады.

Егер жүктеме симметриялы болса, яғни оның фазаларының кедергілері бір біріне тең болса (Z _A= Z _B = Z _C) болса, онда =0, яғни нөлдік сыммен ток жүрмейді. Бұл жағдайда нөлдік сымды сұлбадан алып тастауға болады және желілік пен фазалық токтардың әрекеттік мәндері тең: I_Ж=I_Ф.

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Үш фазалы симметриялы э.қ.к.-тер жүйесі туралы түсініктеме беріңіз.

2. Желілік және нөлдік (бейтарап) сымдар, желілік және фазалық кернеулер мен токтардың анықтамасына тоқталыңыз.

3..Қоректендіргіш пен қабылдағыштың фазаларының жұлдызша сұлбасы бойынша жалғануын қарастырып, векторлық диаграмманы тұрғызыңыз. Бейтарап сымның қызметіне тоқталыңыз.

4 Үш фазалық симметриялы жүйедегі желілік және фазалық кернеулер, токтар арасындағы қатынастар қандай түрде болады?

№13 Дәріс. Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануы. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбектегі симметриялы емес режим және оны есептеу

Қоректендіргіштің фазаларын үшбұрыш сұлбасы бойынша қосу үшін бір фазаның аяқы ұшын екінші фазаның басқы ұшымен, екінші фазаның аяқы ұшын үшінші фазаның басқы ұшымен, ал үшінші фазаның аяқы ұшын бір фазаның басқы ұшымен қосады (40-сурет). Сұлбада бейтарап сым болмайды. Сондықтан қоректендіргіштің желілік кернеулері оның фазалық кернеулеріне тең болады:

Егер U _AB = Е _А, U _BC = E _B, U _CA = E _C. Ом заңы бойынша қабылдағыштың фазалық токтары:

I _АВ= / Z _AВ = U _AВ/ Z _AВ, I _BС= E _B/ Z _BС= U _BС/ Z _BС, I _CА= E _C/ Z _CА= U _CА / Z _CA.

Егер қабылдағыш симметриялы (Z _AВ= Z _BС = Z _CА) болса, онда барлық фазалық токтардың әрекеттік мәндері бірдей болады және олардың желілік кернеулерге байланысты фазалық ығысулары да бірдей болады.

Кирхгофтың бірінші заңы бойынша желілік токтар: I _A= I _AB - I _CA, I _B= I _BC - I _AB, I _C= I _CA - I _BC. Бұл желілік және фазалық токтардың комплекстік мәндері үшін құрылған векторлық диаграмадағы токтар үшбұрышынан желілік токтардың модулдері мен фазалық токтардың модулдері арасында мынадай байланыс барынан көрінеді:

I_ж =2I_Фcos30˚= I_Ф.

Үш фазалы тізбектің операторы деп модулі 1-ге тең, фазасы 120⁰-қа тең комплекс санды атайды. Оны 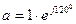,, ;Үш вектор 1, а, а² симметриялы үш фазалы жүйе құрайды (41-сурет), сондықтан ; Кез-келген векторды операторға а көбейткенде ол вектордың модулі өзгермейді, бірақ ол 120⁰-қа бұрылады. Ал векторды а² көбейтсек, онда ол 240⁰ бұрылады. Операторды а пайдаланып E _B және E _C –ні E _A арқылы өрнектеуге болады: E _B= a² E _A, E _C= a E _A (42-сурет).

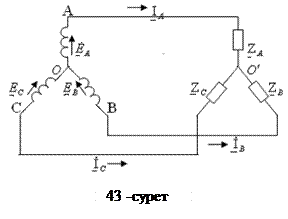Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек (43-сурет). Егер жүктеме симметриялы емес (Z _A ≠ Z _B ≠ Z _C) болса, сұлбаның екі түйіні (О және О′ нүктелері) арасында потенциалдар айырымы - U_00′ кернеуі пайда болады. Бұл кернеуді анықтау үшін екі түйіндік потенциалдар тәсілін қолданамыз. Бұл тәсіл бойынша:

U_00′ = (Е _А Y _A + E _B Y _B + E _C Y _C)/(Y _A+ Y _B+ Y _C)= =(Е _А Y _A+ + a² E _A Y _B + a E _A Y _C)/(Y _A+ Y _B+ Y _C)= = Е _А (Y _A + a² Y _B + a Y _C)/(Y _A+ Y _B+ Y _C), мұндағы Y _A=1/ Z _A, Y _B=1/ Z _B, Y _C=1/ Z _C – жүктеменің фазаларының комплекстік өткізгіштері.

Желілік токтарды анықтаймыз: I _A =U_A0′ / Z _A , I _B = U_B0′ / Z _B, I _C= U_C0′ / Z _C.

Бұл өрнектердегі кернеулер

U_A0′ = Е _А- U_00′, U_B0′ = Е _B- U_00′, U_С0′ = Е _С- U_00′.

Егер Z _A = Z _B = Z _C болса, онда Y _A = Y _B= Y _C= Y. Сондықтан U_00′ = Е _А Y (1 + a² + a)/3 Y =0.

Бұл жағдайда U_A0′ = Е _А, U_B0′ = Е _{B ′}, U_C0′ = Е _С, сол себепті де I _A = Е _А / Z _A , I _B = Е _B / Z _B, I _C= Е _С / Z _C;

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 4,6,7,9,14 ]

Бақылау сұрақтары:

1.Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануына түсініктеме беріңіз. Токтар үшін векторлық диаграмма тұрғызыңыз.

2. Желілік токтарды фазалық токтар арқылы қалай табуға болады? Жүйе симметриялы болған кезде желілік токтардың модульдары мен фазалық токтардың модульдарының арасындағы қатынас қандай болады?

3. Үш фазалы тізбектің операторы дегенімз не? Оператор арқылы симметриялы э.қ.к.-тер қалай бейнелінеді?

4. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек туралы түсініктеме беріңіз және есеп тәсіліне тоқталыңыз.

5. Осы тізбек симметриялы болса, онда есептеу жұмысы қалай жүргізіледі?

№14 Дәріс. Үш фазалы тізбектердің қуаттары және оларды өлшеу. Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектер. Үш фазалы желінің балама сұлбасы

Үш фазалы тізбектің активті қуаты жүктеменің фазаларының активті қуаттарының және нөлдік сымның кедергісінде бөлінетін активті қуаттың қосындысына тең:

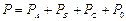,[Вт].

Үш фазалы тізбектің реактивті қуаты:

, [ВАр].

Толық қуат: 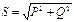, [ВА].

Жүктеме симметриялы болса болса, онда: ,, ,.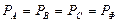

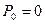Фазалық активті қуат: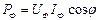; Фазалық реактивті қуат: . Үш фазалы тізбектің активті және реактивті қуаты: , .

Үш фазалы тізбектің толық қуаты: ;

Жүктеменің фазаларының өзара жалғану сұлбаларына (жұлдызша немесе үшбұрыш) байланыссыз үш фазалы тізбектің қуаттарын желілік кернеу мен желілік ток арқылы анықтауға болады.: , , ;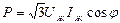

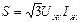Үш фазалы тізбектің активті қуатын өлшеу. Егер үш фазалы тізбекте нөлдік сым болса, бірақ жүктеменің фазаларының кедергілері Z _A, Z _B, Z _C бірдей болмаса, онда тізбектің активті қуатын өлшеу үшін үш ваттметр қолданылады (44-сурет).

44-сурет

45-сурет

Тізбектің активті қуаты осы үш ваттметр көрсетуінің қосындысына тең.

Егер тізбектің нөлдік сымы болмаса, онда активті қуатты өлшеу үшін екі ваттметр қолданылады (45-сурет). Бұл екі ваттметрдің көрсетуілері көбінесе бірдей болмайды. Бұл жағдайда үш фазалық жүйенің қуаты екі ваттметрдің көрсетулерінің алгебралық қосындысына тең.

Айталық, бірінші ваттметрдің көрсетуі P₁=Re[ U _AC Ī_A], ал екінші ваттметрдің көрсетуі P₂= Re[ U _BC Ī_B]. Бұл жағдайда ваттметрлердің көрсетулерінің қосындысы

U _AC Ī_A+ U _BC Ī_B=(U _A - U _C) Ī_A+(U _B - U _C) Ī_B= U _A Ī+ U _B Ī_B+ U _C Ī_C.

Соңғы өрнек үш фазаның активті қуаттарының қосындысын көрсетеді.

Егер жүктеме симметриялы болса, онда бір фазаның активті қуатын үшке көбейтеміз.

Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектерді есептеу бір фазалық синусоидалық токтың индуктивтік байланысы бар тізбегінің есебіне ұқсас жүргізіледі.

Үш фазалы желінің балама сұлбасын тұрғызу үшін желінің өнбойында болып жатқан электромагниттік құбылыстар есепке алынуы керек. Магниттік құбылыстарды индуктивтілк, электр өрісііне байланысты құбылыстарды сыйымдылық, ал жылу бөліну құбылысын кедергі арқылы сипаттайды.

Үш фазалы желінің балама сұлбасына оның сымдарының индуктивтілігі және сымдар арасындағы өзара индуктивтілік, сымдар мен жер арасындағы сиымдылық, сымдардың арасындағы сиымдылық, сымдарың активті кедергілері және оқшаулағыштардың (изоляцияның) өткізгіштері енуі тиіс. 46 –суретте үш фазалы желінің бір фазасының «П» және «Т» тәрізді балама сұлбалары келтірілген. Суретте көрсетілген индуктивтілік L_ф симметриялы үш фазалы желінің индуктивтілігі деп

46- сурет

аталады: L_ф=L_з - М_з. Мұндағы L_з -сымның индуктивтілігі, ал М_з. – сымдар арасындағы өзара индуктивтілік. Желі симметриялы болу үшін, яғни L_з және М_з барлық фазалар үшін бірдей болуы үшін, желінің ұзындығын үшке бөліеді де, сымдардың өзара орналасу ретін әр бөлікте өзгертіп отырады. Бұл тәсілді сымдардың транспозициясы деп аталады.

Суретте көрсетілген сиымдылық С_ф фаза сыйымдылығы деп аталады: С_ф =С_о +3С_м. Мұндағы С_о- сым мен жер арасындағы сыйымдылық, ал С_м – сымдар арасындағы сыйымдылық. Желі сымдарын транспозициялау арқасында С_ф мәні үш фаза үшін бірдей болады.

Суреттегі кедергі R - сымның активті кедергісі. Желі симметриялы болғандықтан бейтарап сыммен ток жүрмейді. Сондықтан бейтарап сымның кедергісі сұлбаға енбеді.

Үш фазалы жүйенің артықшылықтары: а) Электр энергиясын бір фазалық жүйемен алыс қашықтыққа жеткізу үшін қажетті алты сым орнына үш фазалық жүйемен тасымалдағанда небәрі үш сым ғана керек болады, яғни үш фазалық жүйемен тасымалдаған экономикалық жағынан тиімді;

б) Үш фазалы электр қондырғылары құрылысы жағынан қарапайым, бағасы арзан, жұмыс істеуі сенімді болады;

в) Үш фазалы жүктеме симмериялы болса, онда жүйенің лездік куатының мәні период ішінде өзгермейді.

Негізгі әдебиеттер: [1(162-184), 3(397-405)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Үш фазалы тізбектің активті, реактивті және толық куаты қалай анықталады?

2. Үш фазалы тізбектің активті ңуатын қалай өлшейді?

3 Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектерді есептеу қалай жүргізіледі?

4.Үш фазалы желінің балама сұлбаларына түсініктеме беріңіз

5. Үш фазалы жүйенің бір фазалы жүйеге қарағанда қандай артықшылықтары бар?

№15 Дәріс. Периодтық синусоидалы емес тоқ тізбектері

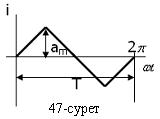Синусоидалы емес ток немесе кернеу деп уақытқа тәуелді синусоидалы емес заңдылықпен өзгеретін ток пен кернеуді айтады. Тізбекте синусоидалы емес ток немесе кернеу қоректендіргіш синусоидалы емес э.қ.к. өндіретін болса немесе тізбектің элементтерінің кем дегенде біреуі сызықты емес болса, немесе олар уеқытқа тәуелді периодты түрде өзгерген жағдайларда пайда болады. Синусоидалы емес токтар немесе кернеулер периодты қисықтар немесе периодты емес қисықтар арқылы сипатталады. Біз периодты синусоидалы емес токтар немесе кернеулер (47-сурет) тізбегін қарастырамыз. Сызықты тізбекке периодты синусоидалы емес э.қ.к, ток немесе кернеу әсер еткен кезде болатын құбылыстарды зерттеу жұмыстарын жеңілдету мақсатында синусоидалы емес э.қ.к-тің, токтың немесе кернеудің қисықтарын Фурье қатарларына жіктеу тиімді.

Дата добавления: 2014-01-07