
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дебиеттер тізімі 4 страница
|
|
|
|
Негізгі әдебиеттер: [1(72-78, 94-98), 2(145-152)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1. Активті кедергісі бар тізбек үшін ток және фазалық ығысу қалай анықталады? Бұл тізбек үшін векторлық диаграмма тұрғызыңыз. Тізбектің лездік қуатын аналитикалық және графикалық жолмен сипаттаңыз. Активті қуат неге тең?
2.Идеал индуктивті элементі бар тізбек үшін кернеуді, индуктивті кедергіні және фазалық ығысуды қалай анықталады? Векторлық диаграммада кернеу мен токтың векторларының өзара орналасуына түсініктеме беріңіз.Лездік қуаттың сипаты қандай? Индуктивті реактивті қуат қалай анықталады?
3. Идеал сиымдылық элемент бар тізбек үшін ток, сиымдылық кедергі және фазалық ығысу қалай анықталады? Бұл тізбек үшін векторлық диаграмма тұрғызыңыз. Тізбектің лездік қуатын аналитикалық және графикалық жолмен сипаттаңыз. Сыйымдылық реактивті қуат неге тең?
№7 Дәріс. Активті кедергісі, идеал индуктивті элемент және сыйымдылық элементтер бірізді жалғанған тізбек
Бірізді жалғанған r, L және C элементтерден тұратын электр тізбегі арқылы (20-сурет) синусоидалы ток i=Imsin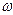 t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
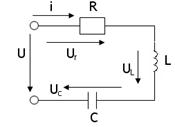 20-сурет 20-сурет
| u= ri+ L + + = rImsin = rImsin t+Im t+Im Lcos Lcos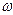 t - t - 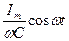 немесе
u=rImsin немесе
u=rImsin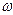 t+Im t+Im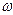 Lsin( Lsin(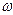 t+90o)+ t+90o)+ =Umrsin =Umrsin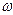 t+UmLsin( t+UmLsin(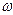 t++90o) +Umcsin( t++90o) +Umcsin(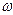 t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I  , ,
|
U r I, U L
I, U L I, U C=
I, U C=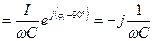 I, U =
I, U =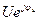 , j=ej90˚, -j=e --j90˚
, j=ej90˚, -j=e --j90˚
Комплекстік кернеулер мен токты векторлық диаграммада көрсетейік. Фаза бойынша U r кернеу I токпен дәл келеді, U L фаза бойынша I токтан 90o алға озады, ал U C кернеуі фаза бойынша I токтан 90o
 21-сурет
21-сурет
 22-сурет 22-сурет
 23-сурет
23-сурет
| кеш қалады (17-сурет). U r, U L, және U C векторларды қосу нәтижесінде U векторын аламыз. Бұл векторлар кернеулер үшбұрышын құрайды (21-сурет). Оның бір катетін активті кернеу Ur, екінші катеті реактивті кернеу Up= UL – UC , ал гипотенузаны толық кернеу U құрайды. Пифагор теоремасы бойынша: U= = = = = = =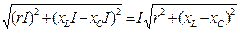 =Iz, мұндағы z =Iz, мұндағы z  - толық кедергі. U кернеуінің векторымен I ток векторының арасындағы бұрыш - фазалық ығысуды φ анықтайды: φ= arctg - толық кедергі. U кернеуінің векторымен I ток векторының арасындағы бұрыш - фазалық ығысуды φ анықтайды: φ= arctg . Егер UL<UC болса, онда φ таңбасы теріс болады.
Кернеулер үшбұрышынан активті кернеуді Ua және реактивті кернеуді Up толық кернеу U мен фазалық ығысу φ арқылы табуға болады: Ua= Ur= Ucos φ; Up= Usin φ.
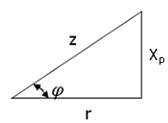
Тізбектің толық кедергісінің z формуласындағы xL – xC айырмасын реактивті кедергі xp деп атайды, яғни xp= xL – xC..
Толық кедергінің өрнегі бір катеті активті кедергіге r, екінші катеті реактивті кедергіге xp, ал гипотенузасы толық кедергіге z тең тікбұрышты үшбұрышқа сәйкес келеді. Бұл үшбұрышты кедергілер үшбұрышы деп атайды (22-сурет).
Бұл үшбұрыштан фазалық ығысу φ= arctg xp / r. Оның таңбасы xL < xC болғанда теріс болады.
Егер z және φ белгілі болса, онда кедергілер үшбұрышынан r = z cos φ; xp= z sin φ. . Егер UL<UC болса, онда φ таңбасы теріс болады.
Кернеулер үшбұрышынан активті кернеуді Ua және реактивті кернеуді Up толық кернеу U мен фазалық ығысу φ арқылы табуға болады: Ua= Ur= Ucos φ; Up= Usin φ.
Тізбектің толық кедергісінің z формуласындағы xL – xC айырмасын реактивті кедергі xp деп атайды, яғни xp= xL – xC..
Толық кедергінің өрнегі бір катеті активті кедергіге r, екінші катеті реактивті кедергіге xp, ал гипотенузасы толық кедергіге z тең тікбұрышты үшбұрышқа сәйкес келеді. Бұл үшбұрышты кедергілер үшбұрышы деп атайды (22-сурет).
Бұл үшбұрыштан фазалық ығысу φ= arctg xp / r. Оның таңбасы xL < xC болғанда теріс болады.
Егер z және φ белгілі болса, онда кедергілер үшбұрышынан r = z cos φ; xp= z sin φ.
|
Лездік қуат: p= ui=  -
-
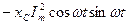 =
= , мұндағы pa=
, мұндағы pa= -активті лездік қуат; ал pp=
-активті лездік қуат; ал pp= - реактивті лездік қуат;
- реактивті лездік қуат;
Активті лездік қуат pa=UaI – UaIcos2 t= UIcos
t= UIcos - UIcos
- UIcos cos2
cos2 t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады
t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады . Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos
. Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos -ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos
-ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos = uaI= rI2.
= uaI= rI2.
Индуктивті лездік қуат: pL= , сиымдылық лездік қуат: pC=
, сиымдылық лездік қуат: pC= . Бұл қуаттардың фазалары қарама-қарсы. Тізбектің реактивті қуаты:
. Бұл қуаттардың фазалары қарама-қарсы. Тізбектің реактивті қуаты:
pp= pL+pC=(xL – xC) I2 sin2 t = xp I2 sin2
t = xp I2 sin2 t = Up I sin2
t = Up I sin2 t= UI sinφ sin2
t= UI sinφ sin2 t.
t.
Лездік қуат: p= UIcos - UIcos
- UIcos cos2
cos2 t + UIsin
t + UIsin sin2
sin2 t = UIcos
t = UIcos + UIsin(2
+ UIsin(2 t+
t+ - 90o), яғни
- 90o), яғни
 24-сурет
24-сурет
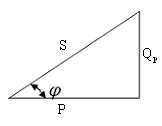
| ол тұрақты құраушыдан және айнымалы құраушыдан тұрады (24-сурет). Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].
Лездік реактивті қуаттың амплитудасын (UIsin (24-сурет). Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].
Лездік реактивті қуаттың амплитудасын (UIsin ) реактивті қуат Qp= UIsin ) реактивті қуат Qp= UIsin деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Qp= QL – QC= xLI2 – xCI2= ULI – UC I =Up I. деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Qp= QL – QC= xLI2 – xCI2= ULI – UC I =Up I.
|
Кедергілер үшбұрышының қабырғаларын I2 көбейтсек, онда қуаттар үшбұрышын аламыз. Оның бір катеті активті қуатқа P, екінші катеті реактивті қуатқа Qp, ал гипотенузасы толық қуатқа S сәйкес келеді. Бұл үшбұрыштан толық қуат:S= , φ= arctg Qp/ P, немесе P= Scos
, φ= arctg Qp/ P, немесе P= Scos , Qp = Ssin
, Qp = Ssin .
.
Әр түрлі электротехникалық қондырғыларда бір мезгілде электр энергиясының жылулық немесе механикалық энергияға айналуының қайтымсыз процестерімен қатар қайтымды процесс- электр энергиясының магнит энергиясына айналуы жүріп жатады. Активті қуат пайдалы жылуға немесе механикалық жұмысқа жұмсалатын болғандықтан электр энергиясының бір бөлігі ғана жұмсалады. Реактивті қуат пайдалы жұмыс жасамайды.
Активті қуаттың толық қуатқа қатынасын электротехникада қуат коэффициенті деп атайды: cos = P/ S.
= P/ S.
Негізгі әдебиеттер: [1(78-86, 94-98), 3(152-156, 190-196)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1. Бірізді жалғанған r, L және C элементтерден тұратын электр тізбек күйінің теңдеуіне түсініктеме беріңіз.
2.Векторлық диаграммада токтың және кернеулердің векторларының өзара орналасуы. Кернеулер үшбұрышы. Активті, реактивті және толық кернеулер.
3. Кедергілер үшбұрышы. Тізбектің активті, реактивті және толық кедергілері.
4. Тізбектің лездік қуаты. Активті, реактивті және толық қуат.
5. Қуаттар үшбұрышы. Қуат коэффициенті.
№8 Дәріс. Активті кедергі, идеал индуктивті элемент және сыйымдылық элементтер параллель жалғанған тізбек
 Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=Umsinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:
Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=Umsinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:
 , немесе i =(Um/r)sinωt+(Um/ωL) sin(ωt-90˚)+ωCUm sin(ωt+90˚).
, немесе i =(Um/r)sinωt+(Um/ωL) sin(ωt-90˚)+ωCUm sin(ωt+90˚).
Комплекстік әрекеттік мәндерге көшейік:
 I =Iejφ, Ia = Iaej0, IL =ILe-j90˚ , IC =ICej90˚ , мұндағы Ia=U/r, IL=U/ ωL,
I =Iejφ, Ia = Iaej0, IL =ILe-j90˚ , IC =ICej90˚ , мұндағы Ia=U/r, IL=U/ ωL,
IC=U ωC – токтардың модульдері, ал U=Um/ . Алынған теңдеуден активті кедергідегі токтың фаза бойынша кернеумен бірдей болатынын көреміз. Ток индуктивті элементте фаза бойынша 90˚ артта қалады, ал ток сыйымдылық элементтегі кернеуден фаза бойынша 90˚ озады. Кернеу мен токтардың векторларының өзара орналасуы 26-суреттегі векторлық диаграммада көрсетілген. Индуктивті ток IL пен сыйымдылық токтың IC фазалары қарама-қарсы болғандықтан олар бір бірінен алынады. Олардың айырымын реактивті ток деп атайды: Ip= IL- IC. Векторлық диаграммадан активті ток Ia, реактивті ток Ip және тізбектің толық тогы I тікбұрышты үшбұрыш құрайтынын көреміз. Бұл токтар үшбұрышының катеттерін Ia және Ip токтары құрайды да, ал гипотенузасы I тогы болады. Пифагор теоремасы бойынша:
. Алынған теңдеуден активті кедергідегі токтың фаза бойынша кернеумен бірдей болатынын көреміз. Ток индуктивті элементте фаза бойынша 90˚ артта қалады, ал ток сыйымдылық элементтегі кернеуден фаза бойынша 90˚ озады. Кернеу мен токтардың векторларының өзара орналасуы 26-суреттегі векторлық диаграммада көрсетілген. Индуктивті ток IL пен сыйымдылық токтың IC фазалары қарама-қарсы болғандықтан олар бір бірінен алынады. Олардың айырымын реактивті ток деп атайды: Ip= IL- IC. Векторлық диаграммадан активті ток Ia, реактивті ток Ip және тізбектің толық тогы I тікбұрышты үшбұрыш құрайтынын көреміз. Бұл токтар үшбұрышының катеттерін Ia және Ip токтары құрайды да, ал гипотенузасы I тогы болады. Пифагор теоремасы бойынша: ,
,  ,
,
мұндағы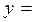
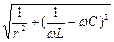
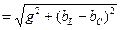 – тізбектің толық өткізгіштігі. Бұл өрнектегі g=1/r - активті өткізгіштік деп, bL=1/xL=1/ ωL реактивті индуктивті өткізгіштік деп, ал bC=1/xC=1/ ωC реактивті сыйымдылық өткізгіштік деп аталады.
– тізбектің толық өткізгіштігі. Бұл өрнектегі g=1/r - активті өткізгіштік деп, bL=1/xL=1/ ωL реактивті индуктивті өткізгіштік деп, ал bC=1/xC=1/ ωC реактивті сыйымдылық өткізгіштік деп аталады.
Токтар үшбұрышынан тізбектегі кернеудің U толық токтан I фаза бойынша қаншалықты ығысқандығын табуға болады:  . Егер bL > bC болса φ таңбасы оң, ал bL < bC болғанда таңбасы теріс болады.
. Егер bL > bC болса φ таңбасы оң, ал bL < bC болғанда таңбасы теріс болады.
Егер толық ток I және φ белгілі болса, онда Ia= Icosφ, Ip= Isinφ.
 27-сурет
27-сурет
| Тізбектің толық өткізгіштігінің өрнегі бір катеті активті өткізгіштікке g тең, екінші катеті реактивті өткізгіштікке тең b (b= bL - bC), ал гипотенузасы толық өткізгіштікке y тең тікбұрышты үшбұрышқа сәйкес келеді(27-сурет). Бұл үшбұрышты өткізгіштер үшбұрышыдеп аталады Ток пен кернеу арасындағы фазалық ығысуды өткізгіштер үшбұрышы арқылы табуға болады: φ =arctg (bL - bC)/g. Бұл өрнектен фазалық ығысу индуктивті және сиымдылық өткізгіштіктердің өзара қарым-қатынасына байланысты екендігі көрінеді. |
Егер b >0 болса, онда реактивті өткізгіштік b индуктивті сипатта, ал bL < 0 сыйымдылық сипатта болады. Егер b = 0 болса, онда тізбекте токтар резонансы болды.
Егер y және φ белгілі болса, онда g= ycos φ, b= ysin φ.
Токтарды да, қуаттарды да өткізгіштіктер арқылы есептеуге болады: активті ток Ia = U g, реактивті индуктивті ток IL = U bL,, реактивті сыйымдылық ток IC = U bC, ал тізбектің реактивті тогы Ip= U b, толық ток I=U y.
Тізбекте бөлінетін активті қуат P=U2 g, реактивті индуктивті қуат QL=U2 bL,, реактивті сыйымдылық қуат QC= U2 bC,, толық қуат S= U2 y.
Негізгі әдебиеттер: [1(86-91), 3(167-171)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1.Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбек күйінің теңдеуі. Активті, реактивті және толық токтар.
2. Векторлық диаграмма. Токтар үшбұрышы.
3.Тізбектің активті, реактивті және толық өткізгіштіктері. Өткізгіштіктер үшбұрышы.
4.Фазалық ығысу. Тізбектегі энергетикалық үрдістер.Активті, реактивті және толық қуаттар.
№9 Дәріс. Синусоидалы ток тізбегін есептеудің комплекстік тәсілі.
 Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
А  , мұндағы
, мұндағы  b/a.
b/a.
Егер  , онда
, онда 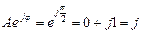 . Егер
. Егер  , онда
, онда 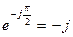
Кез-келген векторды  -ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал -
-ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал - -ға көбейткенде векторды - 90о-қа бұрады (28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне (I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. I m r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен I m jωL, ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен I m(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен E m айырбастаймыз.
-ға көбейткенде векторды - 90о-қа бұрады (28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне (I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. I m r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен I m jωL, ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен I m(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен E m айырбастаймыз.
29-суретте көрсетілген тізбекке Кирхгофтың екінші заңы бойынша лездік мәндер үшін теңдеу құрайық: ua+ uL+ uC= e, немесе
I m r 
Теңдеуді комплекстік түрде жазайық: I m r + I m jωL - I m(j/ωC) = E m, I m [ r + j(ωL -- 1 /ωC)] = E m,
бұдан I m = E m / [ r +j (ωL -- 1 /ωC)]= E m / Z.
Бұл теңдеудің оң жағын да, сол жағын да √2 бөлсек, онда комплекстік әрекеттік мәндер үшін Ом заңын аламыз: I = E / Z. Мұндағы Z – тізбектің комплекстік кедергісі: Z =[ r +j(ωL -- 1 /ωC)]= r+jx = zej φ. Комплекстік кедергінің нақты бөлігі активті кедергіге r, ал жорамал бөлігі реактивті кедергіге x = (ωL -- 1 /ωC) тең. Комплекстік кедергінің модулі  .
.
Комплекстік өткізгіштік деп комплекстік кедергіге кері шаманы айтады:
 ,
, 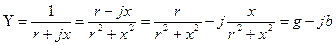
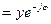 , мұндағы
, мұндағы 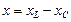 ,
,
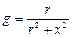 - активті өткізгіштік,
- активті өткізгіштік,  - реактивті өткізгіштік,
- реактивті өткізгіштік, 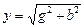 - толық өткізгіштік.
- толық өткізгіштік.
Ом заңын комплекстік өткізгіштік арқылы жазайық: I = U Y, I = U g – U b= I a + I p.
Сонымен электр тізбегінің толық өткізгіштігі нақты бөлігі активті өткізгіштікке, ал жорамал бөлігі реактивті өткізгіштікке тең комплекс сан ретінде жазылады.
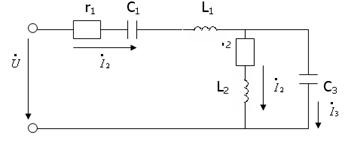 30-сурет
30-сурет
| 30-суретте көрсетілген тізбектің тармақтарының комплекстік кедергілерін жазайық. Ол үшін алдымен активті және реактивті кедергілердің комплекстік түрде жазылуын көрсетейік:  = r, XL = r, XL ,. ,.
|
XC
Тізбектің тармақтарының комплекстік кедергілері:

Тізбектің толық комплекстік кедергісі:
Комплекстік қуат деп кернеудің комплекстік әрекеттік мәнін түйіндес токтың комплекстік әрекеттік мәніне көбейткенге тең: 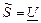 Ỉ. Берілген комплекстік токқатүйіндестоктыңмодулі осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токтыайтады. Айталық,
Ỉ. Берілген комплекстік токқатүйіндестоктыңмодулі осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токтыайтады. Айталық,  - берілген ток болса, онда түйіндес ток Ỉ
- берілген ток болса, онда түйіндес ток Ỉ .
.
Егер 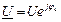 болған жағдайда
болған жағдайда  , мұндағы
, мұндағы
P = UIcosφ - активті қуат;  = UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.
= UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.
Комплекстік қуаттың көрсеткіш түрде жазылуы: =sejφ, мұндағы
=sejφ, мұндағы  ,
,  .
.
Синусоидалы ток тізбегіндегі қуаттар тепе-теңдігі мынаны білдіреді: біріншіден, тізбектегі барлық қоректендіргіштердің активті қуаттарының алгебралық қосындысы сол тізбектегі резистивті элементтердің активті қуаттарының арифметикалық қуаттарының қосындысына тең:
∑UқорIқор cos(φu – φi)= ∑rIr 2 немесе ∑Pқор = ∑Pr,
екіншіден, тізбектегі барлық қоректендіргіштердің реактивті қуаттарының алгебралық қосындысы сол тізбектегі индуктивті элементтердің реактивті қуаттарының арифметикалық қосындысы мен сыйымдылық элементтердің реактивті қуаттарының арифметикалық қосындысының айырмасына тең: ∑UқорIқор sin(φu – φi)= ∑ x LI2 L -∑ x CI2 C, немесе ∑Qқор =∑QL - ∑QC.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1551; Нарушение авторских прав?; Мы поможем в написании вашей работы!