Дебиеттер тізімі 2 страница

Электр сұлбаларының топологиялық элементтері. Тармақ деп элементтері бір-бірімен бірізді жалғанған, бойымен бір ғана тоқ жүретін тізбек бөлігін айтамыз. Түйін деп кем дегенде үш тармақтың түйіскен нүктесін айтады. Контур деп бірнеше тармақ арқылы өтетін тізбектің тұйық бөлігін айтады.

Тұрақты тоқ көздері. Электр тізбегін талдау кезінде электр энергия көздерін мынадай есептік эквивалентпен (баламамен) айырбастайды: мәні реалды энергия көзінің ішкі кедергісіне тең және өзімен бірізді жалғанған кедергісі R_i бар электр қозғаушы күш көзімен (э.қ.к. көзі) немесе мәні реалды энергия көзінің ішкі кедергісіне тең және өзімен параллел жалғанған кедергісі R_i бар ток көзімен айырбастайды (1а және 1б сурет). Реалды э.қ.к. көзінің э.қ.к.-і Е болса, онда оның қысқыштарының арасындағы кернеу U=E-I∙R_i , яғни токқа тәуелді. Бұл U= f (I) тәуелдігін тізбектің сыртқы сипаттамасы деп атайды(1ә -сурет). Реалды э.қ.к. көзінің R_i мәні өте аз болатындықтан кернеудің азаю деңгейі тізбектегі токқа тікелей байланысты. Идеал э.қ.к. көзі үшін R_i =0, U=E, яғни оның қысқыштарының арасындағы кернеу әр уақытта тұрақты және ол арқылы жүретін токқа тәуелсіз.

Реалды ток көзі үшін J=I+U/R_i = I+I∙R_ж /R_i = I(1+ R_ж /R_i), мұндағы J=I_k=E/R_i -ток көзінің қысқаша тұйықталу тогы. Егер R_i →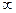, E →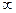 болса, онда J=E/R_i қысқаша тұйықталу тогын береді. Ток көзінің ішкі кедергісі өте үлкен (R_i →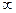)болып және көп жағдайда R_i >> R_ж болса, бұл жағдайда ток көзін идеалды дейді және I=J. Ток көзі бар тізбектің сыртқы сипаттамасы 1в-суретте көрсетілген.

Сонымен идеалды Э.Қ.К. көзі жүктемеге мәні тұрақты, жүктемеге тәуелді өзгермейтін кернеу берсе, ал идеалды ток көзі жүктемеге мәні тұрақты ток беріп отырады.

а) ә) б) в)

1-сурет

Ом заңы. а) Тармақталмаған тізбекте э.қ.к. көзі болмаған жағдайда: I=U/R.

ә)Тармақталмаған тізбекте э.қ.к. көзі болған жағдайда: I=(U + E)/R. Өрнектегі «+» таңбасы Е мен I бағыттары бағыттас болғанда қойылады,ал «-» таңбасы Е мен I бағыттары қарама-қарсы болғанда қойылады.

б)Толық тізбек үшін Ом заңы: I=E/(R_i+R_ж)

Кирхгоф бірінші заңы. Бірінші анықтамасы: Тізбектің кез-келген түйінінде түйіскен токтардың алгебралық қосындысы нөлге тең.Математикалық түрде жазылуы: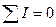. Теңдеу құру үшін тұйінге кірген токтардың таңбасын «+», ал шыққан токтардың таңбасын «-» етіп алу керек.

Екінші анықтамасы: Түйінге кірген токтардың арифметикалық қосындысы түйіннен шыққан тоқтардың арифметикалық қосындысына тең.

Кирхгоф екінші заңы. Бірінші анықтамасы: Тұйық контурдағы э.қ.к.-тердің алгебралық қосындысы сол контурдағы кедергілердегі кернеулердің түсулердің алгебралық қосындысына тең. Екінші анықтамасы: Кез-келген тұйық контурдың бойындағы кернеулердің алгебралық қосындысына нөлге тең.

Математикалық түрде жазылуы: ,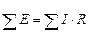

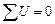
Кирхофтың екінші заңы бойынша теңдеу құрудың реті:

а) Тізбектің тармақтарындағы токтардың бағыттарын өз қалауымызша таңдап аламыз;

ә) Тізбектің контурларын айналу бағытын өз қарауымызша таңдап аламыз;

б) Э.қ.к.- тің алгебралық қосындысын тапқан кезде контурдағы э.қ.к.-нің бағыты контурды айналу бағытымен сәйкес келсе, онда оның таңбасы «+», ал керісінше жағдайда «-» болады;

в) Токтың бағыты контурды айналу бағытымен сәйкес келсе, онда кернеудің түсуінің таңбасы таңбасы «+», ал керісінше жағдайда «-» болады.

Бірінші заң бойынша құрылатын теңдеулер саны: т- 1, мұндағы т- тізбектегі түйіндер саны.

Екінші заң бойынша құрылатын теңдеулер саны: к - (т- 1 ), мұндағы к- тізбектегі тармақтар саны.

Негізгі әдебиеттер: [1(3-29), 3(6-17, 21-26, 35-38, 50-70)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Электротехниканың дамуның қысқаша тарихы.

2.Электр тізбектерінің негізгі ұғымдары. Электр энергия көзі. Электр энергиясын тұтынушылар. Электр тізбектерінің жіктелуі. Электр сұлбалары. Топологиялық ұғымдар: түйін, тармақ, контур.

3.Тұрақты ток тізбегі. Электр қозғаушы күш көзі (э.қ.к) және ток көзі. Олардың сипаттамалары.

4.Тармақталмаған электр тізбегі бөлігі үшін Ом заңы. Э.қ.к-і бар тармақталмаған электр тізбегі бөлігі үшін Ом заңы. Толық тізбек үшін Ом заңы.

5.Кирхгофтың бірінші және екінші заңдары бойынша теңдеулер құру реті.

№2 Дәріс. Бір э.қ.к-і бар тұрақты ток тізбектерін есептеу. Балама түрлендіру тәсілі. Э.қ.к.-тердің бірізді және параллель жалғануы. Электр тізбегінің негізгі принциптері

Бір қоректендіргіші бар электр тізбектерін есептеу үшін балама түрлендіруді қолдануға болады.

а) Кедергілері бірізді жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен R_б айырбастаймыз (2-сурет). Бұл жағдайда тізбектегі ток I= U/R_б. Балама кедергінің R_б мәнін анықтау үшін Кирхгофтың екінші заңы бойынша теңдеу құрамыз: U=U₁+U₂+U₃, мұндағы U₁=I∙R₁ ; U₂=I∙R₂; U₃=I∙R₃; U = I∙R_б. Сонда I∙R_б=I∙R₁+ I∙R₂+ I∙R₃ = I(R₁+R₂+R₃). Бұл теңдеуден R_б=R₁+R₂+R₃. Егер кедергілер бірізді жалғанса, онда балама кедергінің мәні осы кедергілердің арифметикалық қосындысына тең.

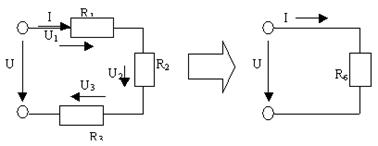
2-сурет

ә) Кедергілері параллель жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен R_б айырбастаймыз. Бұл жағдайда тізбектегі толық ток I= U/R_б. Балама кедергінің R_б мәнін анықтау үшін Кирхгофтың бірінші заңы бойынша теңдеу құрамыз. Параллель тармақтар саны үшеу болған жағдайда I=I₁+I₂+I₃, мұндағы I₁=U/R₁ , I₂=U/R₂ , I₃=U/R₃ – параллель тармақтардағы токтар. Сонда U/R_б=U/R₁+U/R₂+U/R₃. Бұл теңдеуден 1/R_б=1/R₁+1/R₂+1/R₃немесе G_б=G₁+G₂+G₃, мұндағы G_б ,G₁ ,G₂ ,G₃ –тізбектің толық өткізгіштігі және параллель тармақтардың өткізгіштіктері. Жалпы жағдайда 1/R_б=1/ +1/R₂+1/R₃+...+1/ R_n , G_б=G₁+G₂+G₃+…+ G_n.

б) Кедергілері аралас жалғанған электр тізбегін есептеу үшін алдымен параллель тармақтардың кедергісін бір балама кедергімен R₂₃ айырбастаймыз: 1/R₂₃=1/R₂+1/R₃. Сонан кейін R₁ мен R₂₃ бірізді жалғанғандықтан балама кедергімен R_б= R₁+ R₂₃ айырбастаймыз (3-сурет). Тізбектегі толық ток

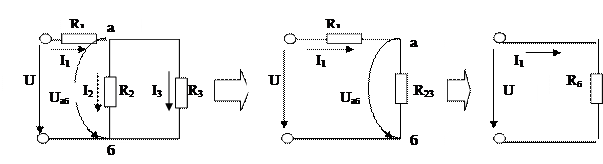I₁=U/R_б=U/(R₁+R₂₃).I₂ мен I₃ токтарын табу үшін U_аб кернеуін табамыз: U_аб=I₁ ∙R₂₃. Бұдан кейін токтарды табуға болады: I₂=U_аб/R₂, I₃=U_аб/R₃.

3-сурет

в) Кедергілердің ұшбұрыштап және жұлдызша жалғануы және оларды балама түрлендіру.

Кейбір жағдайларда есепті жеңілдету мақсатында ұшбұрыштап жалғанған кедергілерді жұлдызша жалғау сұлбасына түрлендіреді. Кейде керісінше түрлендіру де қолданылады. Түрлендіру кезінде мынандай шарттар орындалуы керек:а)Үшбұрыштың А,В,С түйіндеріндегі потенциалдар жұлдызшаның А,В,С потенциалына тең болуы керек; ә)Үшбұрыштың А,В,С түйіндеріне келетін токтар жұлдызшаның осы түйіндерге келетін токтарына тең болуы керек; б)Түрлендіру тізбектің басқа бөлігіне әсер етпеуі керек.

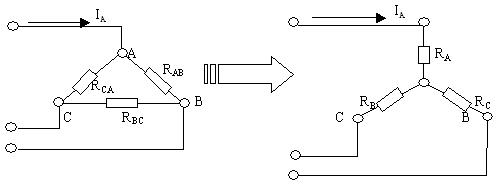
4-сурет

Жұлдызша сұлбаның кедергілерін түрлендірілген үшбұрыш сұлбаның кедергілері арқылы табуға болады: R_A=R_AB ∙R_CA /(R_AB+R_CA+R_BC); R_B=R_AB ∙R_BC /(R_AB+R_CA+R_BC); R_C=R_CA∙R_BC /(R_AB+R_CA+R_BC).

Жұлдызша сұлбаны үшбұрыш сұлбаға түрлендіргенде оның кедергілері төмендегі формулалар арқылы табылады: R_AB=R_A+R_B+R_A∙R_B/R_C; R_BC=R_B+R_C+R_B∙R_C/R_A; R_CA=R_C+R_A+R_C∙R_A/R_B

г)Қоректендіргіштер бірізді жалғанса, онда оларды бір балама қоректендіргішпен айырбастауға (түрлендіруге) болады. Балама қоректендіргіштің э.қ.к.-і E_б қоректендіргіштердің э.қ.к.-терінің алгебралық қосындысына тең, ал ішкі кедергісі R_б қоректендіргіштердің ішкі кедергілерінің арифметикалық қосындысына тең: R_б=R₁+R₂+...+R_n. Бағыттары токтың бағыттымен бағыттас э.қ.к.-тер плюс таңбасымен алынады. Керісінше жағдайда таңбасы минус болады.

д) Параллель жалғанған қоректендіргіштерді бір балама қоректендіргішпен айырбастауға (түрлендіруге) болады (5-сурет).

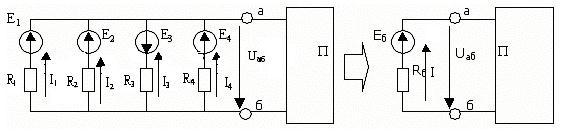
5-сурет

Кирхгофтың бірінші заңы бойынша: I=I₁+I₂+I₃+I₄, немесе

(E_б – U_аб)/R_б =(E₁ – U_аб)/R₁+(E₂ – U_аб)/R₂ +(-E₃ – U_аб)/R₃+(E₄ – U_аб)/R₄. Бұдан

E_б= (E₁G₁+ E₂G₂-E₃G₃+E₄G₄ )/(G₁+G₂+G₃+G₄ ), 1/R_б=1/R₁+1/ R₂+1/ R₃+1/R₄= G₁+G₂+G₃+G₄.

Жалпы жағдайда У_б=/

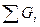
Электр тізбегінің негізгі принциптері (қасиеттері). 1)Беттестіру принципі: Егер тізбекте бірнеше электр қозғаушы күштер болса, онда осы тізбектің кез келген тармағындағы ток осы электр қозғаушы күштердің сол тармақта әрқайсы тудырған токтарының алгебралық қосындысына тең.

2)Теңгеру принципі: Тізбектің тармағындағы кедергіні сандық мәні сол кедергі мен токтың көбейтіндісіне тең, ал бағыты токтың бағытына қарама- қарсы электр қозғаушы күшімен айырбастауға болады.

3)Өзаралық принцип: Тізбектің k тармағына орналасқан э.қ.к. m тармағында I_m (I_m=E_к ∙G_km) тогын тудырса, онда m тармағындағы э.қ.к. Е_m=E_к k тармағында мәні I_m-ге тең I_k (I_к =E_m ∙G_mk)тогын тудырады. G_km, G_mk -өзаралық өткізгіштіктер.

Қуаттар балансы: Тізбектегі қоректендіргіштердің қуаттарының алгебралық қосындысы сол тізбектегі тұтынушылардың қуаттарының арифметикалық қосындысына тең. Қоректендіргіштің қуаты

Р_қ =E∙I, ал тұтынушы қуаты P_т =I² ∙R формулалары арқылы анықталады.

Потенциалдық диаграмма потенциалдың тізбектің өн бойындағы өзгерісін сипаттайды. Тізбектің бір нүктесінің потенциалын нөлге тең деп алады да, қалған нүктелердің потенциалдарын осы нүктенің потенциалымен салыстыра отырып анықтайды. Абцисса осіне масштаб бойынша кедергілерді салады, ал ордината осінде потенциалдарды көрсетеді.

Негізгі әдебиеттер: [1(21-24, 33-35, 42-54), 3(71-74, 80-91, 94-96, 104-108)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бір э.қ.к-і бар электр тізбектерін есептеу. Балама түрлендіру тәсілі. Кедергілердің бірізді, параллель және аралас жалғануы.

2.Кедергілердің жұлдызша және үшбұрыштап жалғануы.

3.Э.қ.к-тердің бірізді және параллель жалғануы. Балама генератордың параметрлері.

4.Электр тізбегінің негізгі принциптері

5.Қуаттар тепе-теңдігі. Потенциалдық диаграмманы құру.

№3 Дәріс. Тұрақты токтың б ірнеше э.қ.к.-тері бар күрделі тізбектерін есептеу тәсілдері. Кирхгоф заңдарын пайдалану арқылы есептеу тәсілі. Контурлық токтар тәсілі. Түйіндік потенциалдар тәсілі

Тұрақты токтың күрделі тізбектерін есептеу үшін мынандай тәсілдерді қолдануға болады:

1) Кирхгофтың заңдарын пайдаланып есептеу тәсілі; 2) Контурлық токтар тәсілі; 3) Түйіндік потенциалдар тәсілі; 4) Екі түйіндік тәсіл; 5) Балама генератор тәсілі.

Кирхофтың заңдарын пайдалану арқылы есептеу тізбектің тармақтарындағы анықталуға тиісті токтарға қатысты теңдеулер құрудан басталады. Құрылатын теңдеулер саны белгісіз токтар санына тең. Кирхгофтың бірінші заңы бойынша құрылатын теңдеулер саны тізбектегі түйін санынан біреуге кем болады, яғни т- 1 тең. Мұндағы т- тізбектегі түйіндер саны. Кирхгофтың екінші заңы бойынша құрылатын теңдеулер саны жалпы құрылатын теңдеулер саны мен бірінші заңы бойынша құрылатын теңдеулер санының айырмасына тең, яғни к -(т- 1 ). Мұндағы к- тізбектегі тармақтар саны. Кирхгофтың екінші заңы бойынша теңдеулер құру кезінде басқа контурға кірмеген тармағы бар тәуелсіз контурлар үшін құруға тырысқан жөн.

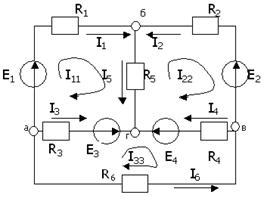
Кирхгофтың заңдары бойынша

6-суретте көрсетілген тізбек үшін теңдеулер құру:

Түйіндер үшін

а) –I₁– I₆ – I₃ =0

б) I₁+I₂ – I₅ =0

в) I₆ – I₂ – I₄ =0

Контурлар үшін

1-контур) E₁ – E₃=I₁∙R₁+I₅∙R₅ – I₃∙R₃

2-контур) –E₂+E₄= -I₂∙R₂+I₄∙R₄ – I₅∙R₅

3-контур) E₃ – E₄= –I₆∙R₆–I₄∙R₄ + I₃∙R₃

Теңдеулер жүйесін өзімізге белгілі әдестер арқылы шешеміз де, I₁,I₂,I₃,I₄,I₅,I₆ токтарды табамыз

6-сурет

2.Контурлық токтар тәсілі. Бұл тәсілді қолданған кезде электр сұлбасының тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді. Контурлық токдеп қарастырылған контурдың барлық тармақтарымен жүреді деп шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер Кирхгофтың екінші заңы бойынша контурлық токтарға байланысты құрылады. Сондықтан есептеу жұмысы көп жеңілдейді.

Контурлық токтар тәсілінің есептеу жұмысында қолданылуын 6-суретте көрсетілген тізбектің тармақтарындағы токтарды анықтау арқылы қарастырайық. Әрбір контур үшін контурлық токтың бағытын өз қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса, онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын алады. Жалпы жағдайда қарастыралатын тізбек үшін теңдеулер мынадай түрде жазылады:

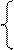Е₁₁= I₁₁∙R₁₁+ I₂₂∙R ₁₂ + I ₃₃∙ R ₁₃

Е₂₂= I₁₁∙R₂₁+ I₂₂∙R ₂₂ + I ₃₃∙ R ₂₃

Е₃₃= I₁₁∙R₃₁+ I₂₂∙R ₃₂ + I ₃₃∙ R ₃₃

Мұндағы Е₁₁, Е₂₂, Е₃₃- бірінші, екінші және үшінші контурлардың контурлық э.қ.к.-тері;

R₁₁, R₂₂, R ₃₃- бірінші, екінші және үшінші контурлардың өзіндік кедергілері,

R₁₁= R₁+R₅ +R₃; R₂₂= R₂+R₄+R₅; R ₃₃= R₆+R₄ +R₃.

R ₁₂=R₂₁- бірінші мен екінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R₁₃= R₃₁- бірінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R ₂₃= R ₃₂- екінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

Теңдеулер 6-суретте көрсетілген тізбек үшін былай жазылады:

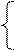E₁ – E₃=I₁₁∙(R₁+R₅ +R₃) – I₂₂∙R₅ –I₃₃∙R₃

– E₂+E₄= I₂₂∙ (R₂+R₄+R₅) – I₃₃∙R₄ –I₁₁∙R₅

E₃ – E₄=I₃₃∙ (R₆+R₄ +R₃) – I₁₁∙R₃– I₂₂∙R₄

Әр теңдеудегі жақшаның ішінде кедергілердің қосындысы контурдың өзіндік кедергісі деп аталады. Теңдеулер жүйесін шешеміз де I_11, I_22, I₃₃ контурлық токтарын табамыз. Тармақтардың токтарын (I₁ ... I₆) контурлық токтар арқылы табамыз:I₁=I₁₁, I₂= –I ₂₂, I₃= I₃₃ – I₁₁, I₄=I₂₂–I₃₃, I₅=I₁₁ – I₂₂, I₆= –I₃₃

3.Түйіндік потенциалдар тәсілі. Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады. Нәтижесінде теңдеулер жүйесі мынадай түрде жазылады:

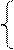φ₁G₁₁ + φ₂G₁₂ + φ₃G₁₃= I₁₁

φ₁G₂₁ + φ₂G₂₂ + φ₃G₂₃= I₂₂

φ₁G₃₁ + φ₂G₃₂ + φ₃G₃₃= I₃₃

φ₁, φ₂, φ₃- бірінші, екінші және үшінші түйіндердің потенциалдары; G₁₁, G₂₂, G₃₃-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; G _km - k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I₁₁, I₂₂, I₃₃- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.

Берілген тізбектің (6-сурет) «г» түйінінің потенциалын нөлге тең деп аламыз.Теңдеулер көрсетілген тізбек үшін былай жазылады:

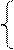φ_а(g₁+g₃+g₆) - φ_бg₁ - φ_вg₆= -E₁g₁-Е₃g₃

φ_б(g₁+g₂+g₅) - φ_аg₁ - φ_вg₂= E₁g₁ + E₂g₂

φ_в(g₂+g₄+g₆) - φ_бg₂ - φ_аg₆= -E₂g₂ -E₄g₄

Мұндағы g₁=1/R ₁, g₂=1/R₂, g₃=1/R₃, g₄=1/R₄, g₅=1/R₅, g₆=1/R₆.

Теңдеулер жүйесін шешу арқылы φ_а, φ_б, φ_в табамыз. Токтардың мәндерін Ом заңы арқылы табамыз:

I₁= (E₁+ U_аб)/R₁ = [E₁+(φ_а - φ_б)]/R₁, I₂= (E₂+ U_вб)/R₂=[E₂+(φ_в- φ_б) ]/R₂, I₃= (E₃+ U_аг)/R₃=[E₃+ (φ_а - φ_г) ]/R₂

I₄= U_вг/R₄=(φ_в - φ_г)/R₄ = φ_в/R₄ I₅= U_бг/R₅=(φ_б - φ_г)/R₄ = φ_б/R₅ I₆= (E₆+ U_ав)/R₆=[ E₆+ (φ_а - φ_в) ]/R₆

Негізгі әдебиеттер: [1(24-33, 35-40), 3(68-71, 74-80, 98-103)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бірнеше э.қ.к-ілері бар күрделі тұрақты ток тізбектерін есептеу тәсілдері. Ом және Кирхгоф заңдарын пайдалану арқылы есептеу.

2.Контурлық токтар тәсілі.

3.Түйіндік потенциалдар тәсілі.

№4 Дәріс. Екі түйіндік тәсіл. Екіұштықтар. Балама генератор тәсілі. Энергияны активті екіұштықтан пассивті екіұштыққа беру

Дата добавления: 2014-01-07