
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дебиеттер тізімі 3 страница
|
|
|
|
 Екі түйіндік тәсіл. Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен Uаб кернеуін табамыз. Тізбектің «б» түйінінің потенциалын нөлге тең деп аламыз. Сонда Uаб=φа – φб = φа – 0 = φа.
Екі түйіндік тәсіл. Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен Uаб кернеуін табамыз. Тізбектің «б» түйінінің потенциалын нөлге тең деп аламыз. Сонда Uаб=φа – φб = φа – 0 = φа.
Тізбектің «а» түйіні үшін: I1 + I2 +I3 + I4=0,
мұндағы I1= (E1 - Uаб)/R1=(E1-φа)/R1,
I2= - Uаб . R2= -φа. R2, I3= (-E3 - Uаб).R 3=(-E3-φа).R3, I4= -φа . R4.
Токтардың өрнектерін теңдеуге қоямыз да, φа табамыз:
φа(g1+g2+g3+g4)= E1g1 – E3g3,
φа=(E1g1 – E3g6)/ (g1+g2+g3+g4).
Табылған φа мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Табылған φа мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Жалпы жағдайда Uаб =∑ Eкg к /∑g к.
Балама генератор тәсілі. Бұл тәсіл күрделі тізбектің бір тармағындағы токты табу үшін қолданылады. Бұл тәсіл бойынша есептеу үшін қарастырылатын тармақты тізбектің басқа бөлігінен бөліктеп аламыз. Қалған бөлікті активті екіұштық деп қарастырамыз. Активті екіұштық дегеніміз екі ғана жалғану ұшы бар, ал ішінде э.қ.к. мен резисторлар бар тізбекті айтамыз (8-сурет).
8-сурет
Егер екіұштықтың ішінде энергия көзі (қоректендіргіш) болмаса, онда оны пассивты екіұштық дейді және оны электр энергиясын қабылдаушы деп санайды. Балама сұлбада пассивты екіұштықты бір кедергімен бейнелейді. Ол кедергіні екіұштықтың ішкі немесе кірістік кедергісі деп атайды.
Тізбектің бөлектенген тармағына байланысты активті екіұштықтықты балама генератормен айырбастауға болады. Бұл генератордың э.қ.к.-і Eб бос жүріс режимі кезінде бөлектенген тармақтың қысқыштарындағы кернеуге Uбж тең, ал , ішкі кедергісі Rб екіұштықтықтың кірістік кедергісі Ri тең.
Қарастырылатын тармақтағы токты табуды мынадай ретпен жүргізген жөн:
а)Eб-ні табу үшін бос жүріс режимін қарастырамыз, яғни тогы анықталуға тиісті тармақты а және б нүктелерінде үзіп, екіұштыдан оны айырып тастаймыз. Онан кейін а және б нүктелерінің арасындағы кернеуді U аб бж есептік жолмен немесе өлшеу арқылы табамыз.
ә) Генератордың ішкі кедергісі Rб табу үшін а және б нүктелеріне байланысты екіұштықтың толық кедергісін анықтаймыз. Ол үшін екіұштықтың сұлбасындағы э.қ.к.-терді алып тастап, олардың орындарын қысқы тұйықтаймыз. Сұлбада тек кедергілерді қалдырамыз.
б) Қарастырылатын тармақтағы токты мына формула бойынша табамыз: I= U аб бж /(Rж+ Ri).
Егер қарастырылатын тармақтың кедергісін нөлге теңестірсе (Rж =0), онда ол үшін қысқаша тұйықталу режимі орын алады. Тармақпен қысқаша тұйықталу тогы (Iқ.т) жүреді: Iқ.т= U аб бж /Rі. Бұдан
Rі.=U аб бж /Iқ.т, яғни ішкі кедергіні табу үшін бос жүріс режимі кезінде өлшенген кернеуді U аб бж қысқаша тұйықталу режимі кезінде өлшенген токқа Iқ.т бөлу керек.
Энергияны активтік екіұштықтан жүктемеге беру. Активті екіұштыққа қосылған жүктемеде Rж бөлінетін қуат P = I2 R = U аб бж Rж /(Rж+ Ri). Қабылдағышқа максимал қуат беру шартын анықтау үшін P-ның Rж бойынша бірінші ретті туындысын тауып,оны нөлге теңейміз. Осыдан Rж = Ri. Демек осы теңдік орындалған жағдайда жүктемеде максимал қуат бөлінеді: Pmax= U2 аб бж /4Rі. Балама генераторда бөлінетін толық қуат Pтол =U аб бж I =U2 аб бж /(Rж+ Ri). Пайдалы әсер коэффициенті (п.ә.к.): η= P/ Pтол = Rж /(Rж+ Ri). Егер Rж = Ri болса, онда η=0,5.
Активті екіұштықтың кірістік кедергісіне Ri тең жұктеме кедергіні Rж келістіру немесе үйлестіру жүктемесі деп атайды.
 Байланыс жүйелерінде, электроникада көп жағдайда қабылдағышқа максимал қуат берудің маңызы зор.
Байланыс жүйелерінде, электроникада көп жағдайда қабылдағышқа максимал қуат берудің маңызы зор.
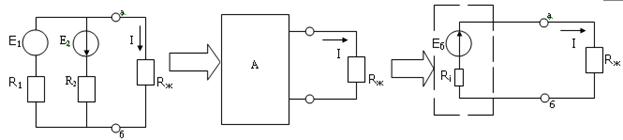
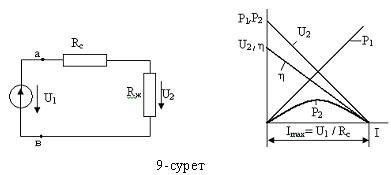
Беріліс желісі арқылы энергияны тасымалдау. Электр желісінің сұлбасы 9а-суретте бейнеленген, мұндағы U1 –желінің басындағы генератордың кернеуі; U2 – желінің соңындағы жүктеменің кернеуі; Rс –желінің сымдарының кедергісі; Rж – жүктеменің кедергісі.
Нақты желілер арқылы үлкен қуат бергенде η = 0,94...0,99 болса онда U2 кернеуі U1 – ден бірнеше пайызға кіші болады. Өте үлкен қуатты алыс қашықтыққа тасымалдағанда п.ә.к.- тің жоғары болуы экономикалық жағынан тиімді. Желінің басындағы қуаттың P1 және жүктемедегі қуаттың P2, п.ә.к пен U2 –нің жүктемедегі токта тәуелді өзгерістерін сипаттайтын сызықтар 9ә-суретте бейнеленген. Олар төмендегі теңдеулер негізінде салынған: P1=U1I; P2=U1I- I2 Rс; η = Rж /(Rж+ Rс); U2=U1 - I Rс. Токтың максималдық мәні Imax = U1 / Rс жүктеменің қысқаша тұйықталу кезінде орын алады.
Желінің п.ә.к.-інің мәні U1 кернеуі неғұрлым жоғары болған сайын, соғұрлым жоғары болады.
Негізгі әдебиеттер: [1(40-41, 54-58), 3(97-98, 109-118)]
Қосымша әдебиеттер: [ 4,5,7,8]
Бақылау сұрақтары:
1.Қандай тізбектерді есептеу үшін екі түйіндік тәсіл қолданылады? Бұл тәсіл бойынша тізбекті есептеу қалай жүргізіледі?
2.Қандай жағдайда тізбекті есептеу үшін балама генератор тәсілін қолданады? Бұл тәсіл бойынша тізбекті 9-сурет есептеу қалай жүргізіледі?
3.Энергияны активті екіұштыдан пассивті екі ұштыға беру. Қабылдағышқа максимал қуат беру шарты қандай? Пайдалы әсер коэффициенті (п.ә.к.) қалай анықталады?
4.Энергияны беріліс желісі арқылы тасымалдаған кезде жүктемедегі кернеудің, жүктемеде бөлінетін қуаттың және п.ә.к.-тің токқа тәуелді өзгерістерінің сипаты қандай?
№5 Дәріс. Синусоидалы ток тізбегі. Синусоидалы шамаларды сипаттайтын параметрлер. Синусоидалы шамалардың мәндері және оларды бейнелеу жолдары
Синусоидалы ток практикада кеңінен қолданылады. Синусоидалы токтың тұрақты токқа қарағанда мынадай артықшылықтары бар: а) Синусоидалы ток өндіретін қондырғылардың (генераторлардың) құрылысы тұрақты ток генераторларына қарағанда қарапайым, жұмыс істеу сенімділігі өте жоғары және бағасы арзан; ә) Трансформаторларды қолдану арқылы синусоидалы кернеудің мәнін өте жоғары дәрежеге көтеруге болатындықтан синусоидалы токты алыс қашықтыққа жеткізу арзанға түседі; б)Синусоидалы токты пайдаланып жұмыс жасайтын электр қондырғылардың құрылысы тұрақты ток қондырғыларына қарағанда әлде қайда қарапайым және арзан.
Синусоидалы ток деп мәні уақытқа тәуелді синусоидалық заңдылықпен өзгеретін токты айтамыз: i=Im*sin( t+
t+ ). Оның графигі 10-суретте көрсетілген. Синусоидалы токты мынадай параметрлер арқылы сипаттауға болады:
). Оның графигі 10-суретте көрсетілген. Синусоидалы токты мынадай параметрлер арқылы сипаттауға болады:
1)Амплитудалық мән (Im, Um, Em ) – синусоидалық шаманың ең үлкен максимал мәні.
2)Периоды (Т) – толық бір тербеліс жасауға кететін уақыт.[c]
3)Жиілік (f) – бір секунда ішінде жасалатын тербеліс саны.[1/c];[Гц] f=1/T; T=1/f
 4)Бұрыштық жиілік (ω) ω =2πf= 2π/ T, [рад/с]
4)Бұрыштық жиілік (ω) ω =2πf= 2π/ T, [рад/с]
5)Фаза ( t+ φ) – кез келген сәттегі синусоидалық шаманың мәнін анықтауға мүмкіндік береді.
t+ φ) – кез келген сәттегі синусоидалық шаманың мәнін анықтауға мүмкіндік береді.
6)Бастапқы фаза φ - синусоидалық шаманың уақыт нөлге тең болған кездегі мәнін анықтауға мүмкіндік береді. Егер φ таңбасы оң болса, онда синусоида ордината осі бойынша солға қарай φ бұрышқа ығысады.,
ТМД елдерінде және Еуропаның біраз елдерінде жиілігі 50Гц синусоидалы кернеу кеңінен қолданылады.
10-сурет Синусоидалы шамалардың мәндері: а) Амплитудалық мән (Im, Um, Em); ә) Лездік мән (i, u, e) - синусоидалы шаманың кез келген сәттегі мәні: i=Imsin( t+
t+ i); u=Umsin(
i); u=Umsin( t+
t+ u); e=Emsin(
u); e=Emsin( t+
t+ e); б) Орташа мән (Iор, Uор, Eор) - синусоидалы шаманың жарты период ішіндегі орташа мәні:
e); б) Орташа мән (Iор, Uор, Eор) - синусоидалы шаманың жарты период ішіндегі орташа мәні:
Iор= =
= =
=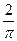 Im=o.638Im: Uор=
Im=o.638Im: Uор= =
= 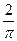 Um=0.638Um.
Um=0.638Um.
Сонымен орташа мән амплитудалық мәннен π/2 есе аз.
в)Әрекеттік мән (I, U, E) немесе орташа квадраттық мән
I=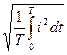 =
= = Im/
= Im/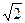 =0.707Im, сол сияқты U= Um/
=0.707Im, сол сияқты U= Um/ 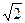 = 0.707Um, Е=0.707Em.
= 0.707Um, Е=0.707Em.
Синусоидалы шамалардың әрекеттік мәндері олардың амплитудалық мәндерінен  есе аз. Синусоидалы ток әрекеттік мәні кедергі арқылы жүрген кезде бір период ішінде синусоидалы ток қанша жылу бөлсе, сонша уақытта сондай жылу бөліп шығаратын тұрақты токтың мәніне тең.
есе аз. Синусоидалы ток әрекеттік мәні кедергі арқылы жүрген кезде бір период ішінде синусоидалы ток қанша жылу бөлсе, сонша уақытта сондай жылу бөліп шығаратын тұрақты токтың мәніне тең.
Өлшеу аспаптардың көпшілігі синусоидалы шаманың әрекеттік мәнін көрсетеді.
Синусоидалы шамаларды бейнелеу жолдары: а ) Тригонометриялық функциялар арқылы бейнелеу: i=Imsin( t+
t+ i); u=Umsin(
i); u=Umsin( t+
t+ u);
u);
ә) Тікбұрыштық координаталарда уақыттық диаграмма арқылы бейнелеу (10-сурет);

 б) Айнымалы вектор арқылы бейнелеу. Тікбұрыштық координаталар жазығында ұзындығы синусоидалы токтың i=Imsin(
б) Айнымалы вектор арқылы бейнелеу. Тікбұрыштық координаталар жазығында ұзындығы синусоидалы токтың i=Imsin( t+
t+ ) амплитудасына Im тең вектор
) амплитудасына Im тең вектор  тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен
тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен  бұрышына ығысқан. Уақыт өткен сайын вектор
бұрышына ығысқан. Уақыт өткен сайын вектор  t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен
t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді. Сол себепті практикада оларды айналдырмайды, оларды бастапқы фазаларына сәйкес жазықтықта өзара орналастырады. Векторларды айналдыру қажеттігі болмағандықтан координаталар осьтерін көрсетудің қажеті болмайды. Бірінші векторды горизонталь немесе вертикал орналастырады да, қалғандарын бастапқы фазаларына сәйкес осы векторға байланысты орналастырады.
анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді. Сол себепті практикада оларды айналдырмайды, оларды бастапқы фазаларына сәйкес жазықтықта өзара орналастырады. Векторларды айналдыру қажеттігі болмағандықтан координаталар осьтерін көрсетудің қажеті болмайды. Бірінші векторды горизонталь немесе вертикал орналастырады да, қалғандарын бастапқы фазаларына сәйкес осы векторға байланысты орналастырады.
Синусоидалы шамалардың векторларлар түрінде бейнелеу оларды геометриялық жолмен қосу немесе алу операциясын орындауға мүмкіндік береді.
в) Синусоидалық шамаларды комплекс сандар арқылы бейнелеу. Синусоидалы шама тригонометиялық функция түрінде берілсін: i=Imsin( t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға Im тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. Im = Imej
t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға Im тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. Im = Imej - комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: Imej(
- комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: Imej( t+
t+ )= Imcos(
)= Imcos( t+
t+ )+ jImsin(
)+ jImsin( t+
t+ ). Жорамал бөлік синусоидалы шамаға тең, яғни синусоидалы шаманы комплекс санның жорамал бөлігі арқылы көрсетуге болады.
). Жорамал бөлік синусоидалы шамаға тең, яғни синусоидалы шаманы комплекс санның жорамал бөлігі арқылы көрсетуге болады.
Синусоидалы шамаларды комплекстік жазықтықта векторлар арқылы көрсету оларды қосып, алуға (геометриялық жолмен) мүмкіндік береді.
Векторлық диаграмма деп жиіліктері бірдей синусоидалық шамаларды комплекстік жазықтықта олардың бастапқы фазаларына сәйкес өзара орналасқан векторларының жиынтығын айтады. Фазалық ығысу деп синусоидалық шамалардың бастапқы фазаларының айырмасын айтады:  =φ2 - φ1.
=φ2 - φ1.
Негізгі әдебиеттер: [1(59-72), 3(136-145)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1.Синусоидалы ток деп қандай токты атайды?. Синусоидалы шамаларды сипаттайтын қандай параметрлерді білесіз?
2.Синусоидалы шамалардың қандай мәндері бар? Олар қалай анықталады?
3. Синусоидалы шамаларды тікбұрыштық координаталарда уақыттық диаграмма арқылы бейнелеуге түсініктеме беріңіз.
4. Синусоидалы шамаларды айнымалы вектор арқылы бейнелеуге түсініктеме беріңіз.
5. Синусоидалық шамаларды комплекс сандар арқылы бейнелеуге түсініктеме беріңіз.
№6 Дәріс. Активті кедергісі бар тізбек. Идеал индуктивті элементі бар тізбек. Идеал сыйымдылық элементі бар тізбек
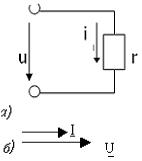
Активті кедергісі бар тізбек. Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін кедергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды.
 13-сурет
13-сурет
| Синусоидалы кернеуді u=Umsin( t+ t+ u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
i=u/r= Um/r sin( u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
i=u/r= Um/r sin( t+ t+ u)=Imsin( u)=Imsin( t+ t+ i). Бұдан токтың әрекеттік мәні
I= (Um/ i). Бұдан токтың әрекеттік мәні
I= (Um/ 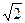 ) /r, ал фазасы ) /r, ал фазасы  i= i= u, Фазалық ығысу u, Фазалық ығысу  = = u- u- i = 0
Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады (13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2 i = 0
Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады (13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2 t = UmIm( t = UmIm( )= )=
| |
 14-сурет
14-сурет
| Лездік қуат тұрақты құраушыдан және екі еселенген жиілікпен өзгеретін айнымалы құраушыдан тұрады (14-сурет). Оның таңбасы әр уақытта оң, яғни электр энергиясы тұрақты түрде басқа түрлі энергияға түрленеді. Период ішіндегі орташа қуатты активті қуат деп атаймыз:
P= , немесе P=UI= =I2 r = , немесе P=UI= =I2 r =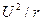 . Активті қуаттың өлшем бірлігі ретінде Ватт (Вт) қабылданған.
Идеал индуктивті элементі бар тізбек (15-сурет). Индуктивтік элемент уақытқа байланысты магнит ағынының өзгерісінен э.қ.к.-тің туу құбылысын және нақты электр тізбегінің элементінде магнит өрісінің . Активті қуаттың өлшем бірлігі ретінде Ватт (Вт) қабылданған.
Идеал индуктивті элементі бар тізбек (15-сурет). Индуктивтік элемент уақытқа байланысты магнит ағынының өзгерісінен э.қ.к.-тің туу құбылысын және нақты электр тізбегінің элементінде магнит өрісінің
| |
энергиясының жинақталу құбылысын есептеуге мүмкіндік береді. Индуктивті орамамен айнымалы ток жүрген кезде оның бойында бағыты сол токқа қарама- қарсы өзіндік э.қ.к. eL пайда болады.
15-сурет 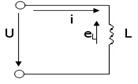
 16-сурет
16-сурет  17-сурет
17-сурет
| Оны берілген кернеу теңгереді: u = -eL, мұндағы eL= - L . Бұдан uL= L . Бұдан uL= L . Егер ток синусоидалы болса i=Imsin . Егер ток синусоидалы болса i=Imsin t, онда uL = L t, онда uL = L = Im = Im Lcos Lcos t = Umsin( t = Umsin( t+90o), мұндағы Um=Im* t+90o), мұндағы Um=Im* L=Im xL, ал xL= L=Im xL, ал xL= L индуктивті кедергі деп аталады.
Фазалық ығысу L индуктивті кедергі деп аталады.
Фазалық ығысу  = = u - u - i =90o, яғни векторлық диаграммада кернеудің U векторы токтың I векторы фаза бойынша 90о-қа озады(16-сурет). Лездік қуат: p = iu = Im sin i =90o, яғни векторлық диаграммада кернеудің U векторы токтың I векторы фаза бойынша 90о-қа озады(16-сурет). Лездік қуат: p = iu = Im sin t Umcos t Umcos t = (sin2ωt) UmIm/2, яғни оның екі еселенген жиілікпен өзгеретіндігін көреміз. Оның амплитудасын QL реактивті индуктивті қуат деп атайды.
QL= t = (sin2ωt) UmIm/2, яғни оның екі еселенген жиілікпен өзгеретіндігін көреміз. Оның амплитудасын QL реактивті индуктивті қуат деп атайды.
QL= 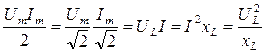 ;
Өлшем бірлігі - вольтампер реактивтік [ВАр]. Периодтың бірінші ширегінде индуктивті элемент электр желісінен энергия алып, оны магнит өрісінің энергиясына айналдырады да, бойына жинайды(17-сурет). Екінші ширекте лездік қуаттың таңбасы теріс, яғни индуктивті элемент бойына жинақтаған магнит энергиясын электр энергиясына түрлендіріп, электр желісіне қайтарады. Үшінші ширекте индуктивті элемент электр желісінен энергия алады да, ;
Өлшем бірлігі - вольтампер реактивтік [ВАр]. Периодтың бірінші ширегінде индуктивті элемент электр желісінен энергия алып, оны магнит өрісінің энергиясына айналдырады да, бойына жинайды(17-сурет). Екінші ширекте лездік қуаттың таңбасы теріс, яғни индуктивті элемент бойына жинақтаған магнит энергиясын электр энергиясына түрлендіріп, электр желісіне қайтарады. Үшінші ширекте индуктивті элемент электр желісінен энергия алады да,
|
төртінші ширекте сол энергияны қайтарады. Период ішіндегі орташа қуат нөлге тең(P=0). Сонымен индуктивті элементте электр энергиясының магнит энергиясына, магнит энергиясының электр энергиясына айналу құбылысы алма кезек жүріп жатады.
Идеал сыйымдылық элементі бар тізбек (18-сурет). Егер сыйымдылық элементке синусоидалы кернеу u = Umsin t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді:
t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді:
 18-сурет
18-сурет
 19-сурет
19-сурет
| q=Cu= СUmsin t. Сыйымдылық элементпен жүретін ток i = dq/dt = C t. Сыйымдылық элементпен жүретін ток i = dq/dt = C . Бұдан Im= UmC . Бұдан Im= UmC = =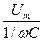 = Um/xc , мұндағы xC= = Um/xc , мұндағы xC=  сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Фазалық ығысу сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Фазалық ығысу  = = u - u - i =0-90o= -90o, яғни векторлық диаграммада сыйымдылық элементпен жүретін токтың I векторы кернеудің U векторынан фаза бойынша 90о-қа озады (19-сурет).
Лездік қуат: p = i u = Imsin( i =0-90o= -90o, яғни векторлық диаграммада сыйымдылық элементпен жүретін токтың I векторы кернеудің U векторынан фаза бойынша 90о-қа озады (19-сурет).
Лездік қуат: p = i u = Imsin( t+90o)Umsin t+90o)Umsin t = (sin2 t = (sin2 t) t)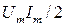 , яғни ол екі еселенген жиілікпен өзгереді Оның амплитудасын реактивті сыйымдылық қуат Qс деп атайды.
QC= , яғни ол екі еселенген жиілікпен өзгереді Оның амплитудасын реактивті сыйымдылық қуат Qс деп атайды.
QC=  ; Өлшем бірлігі- [ВАр] ; Өлшем бірлігі- [ВАр]
|
Конденсатор периодтың бірінші және үшінші ширектерде қоректендіргіштен энергия алып, бойына жинайды(яғни зарядталады). Ал екінші және төртінші ширектерде бойына жинаған энергияны электр желісіне қайтарып береді (17-сурет). Сонымен конденсаторда энергия алмасу құбылыстары жүріп жатады. Период ішіндегі орташа қуат, яғни активті қуат нөлге тең (Р= 0).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1581; Нарушение авторских прав?; Мы поможем в написании вашей работы!