Доказательство. Необходимо доказать, что выполняется равенство

Х2

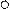
Х1

- не является выпуклым,

т.к. существует точка, ко-

торая ÏD.

является выпуклым.

Определение 2. Крайней точкой выпуклого множества называется точка, принадлежащая этому множеству, но которая не может быть представлена в виде линейной комбинации двух точек, т.е. Х¹lХ1+(1-l)Х2, т.е. не найдутся такие Х1 и Х2, которые образовали бы отрезок, на котором располагалась бы эта точка.

Крайние точки

Свойства:

1. Если D- выпуклое ограниченное множество, имеющее конечное число крайних точек, то любая его точка может быть представлена в виде выпуклой комбинации крайних точек:

Х= a1C1 +a2C2 +…+akCk, где n

å ai =1. i =1

Определение.

Опорной плоскостью (прямой) к множеству D называется плоскость (прямая), имеющая, по крайней мере, с областью одну общую точку. При этом вся область расположена по одну сторону от этой плоскости (прямой).

Определение.

Выпуклым многогранником называется замкнутое выпуклое множество, имеющее конечное число крайних точек, которые называются вершинами.

Симплексом называется n-мерный выпуклый многогранник, имеющий одну n+1 вершину.

Теорема. (Свойство выпуклости допустимых решений задачи нелинейного программирования)

Всякое множество, задаваемое системой линейных неравенств

a11Х1+a12Х2+…+a1nХn Í b1;

a21Х1+a22Х2+…+a2nХn Í b2; (2)

……………………………..

am1Х1+am2Х2+…+amnХn Í bm;

Х1,Х2,…,Хn Ê 0;

является выпуклым.

Х=lХ1+(1-l)Х2, т.е.существуют ли точки Х1 и Х2, которые удовлетворяют системе ограничений (2). Докажем выполнение неравенств (2). Запишем точку Х в координатной форме:

(1) (1)

lХ1 +(1- l)Х1 Возьмём i -тое неравенство и

(1) (1) подставим в него Х

Х= lХ2 +(1- l)Х2

(1) (1)

lХn +(1- l)Хn

Получим:

(1) (2)

ai1 (lХ1 +(1- l)Х1) + ………………………….+

(1) (2)

+………+ ain (lХ1 +(1- l)Хn). Откуда

(1) (1) (2) (2)

l(ai1 Х1 + ….+ ainХn + (1- l) (ai1 Х1 + ….+ ainХn)).

Х1 и Х2 удовлетворяют системе ограничений, значит в сумме всё будет меньше bi, где можно взять любое i Ì [1,m]. Теорема доказана.

2. Максимум функции достигается в крайней точке ОДР.

Теорема. Целевая функция F задачи линейного программирования достигает своего максимального значения в угловой точке ОДР.

Если целевая функция принимает максимальное значение более, чем в одной крайней точке, то она достигает того же значения в каждой точке, являющейся выпуклой линейной комбинацией этих точек.

Доказательство.

Пусть ОДР ограничена и имеет конечное число крайних и угловых точек Х1, Х2, …, Хn.

Пусть Х0-оптимальное решение задачи (1)-(3). Если Х0- крайняя точка, то теорема доказана.

Пусть Х0-точка, являющаяся крайней точкой, но как любая допустимая точка она может быть представлена в виде выпуклой линейной комбинации крайних точек (см. теорему б/д).

ХO= a1C1 +a2C2 +…+aрCр, где р

å ai =1 и ai Ê0.

i =1.

Запишем функцию F(ХO) = F(a1C1 +a2C2 +…+aрCр) = a1 F(Х1) + + a2 F(Х2) + …+ aр F(Хр). Пусть максимум F(Хi)= F(Хk)=M,

где 1Í i Í p.

F(ХO) Í a1М + a2 М +…+ aрМ = (a1 +a2 +…+aр) М = М.

ХO –оптимальная точка. F(ХO) Í М

F(Х0)=M, F(Хk)=M.

F(ХO) Ê М

Хk-угловая точка. Т.О. максимум достигается в Хk.

Предположим, что максимум достигается в нескольких точках:

Х1, Х2,…, Хq, где qÍp.

Пусть Х является выпуклой линейной комбинацией этих точек:

Х= a1C1 +a2C2 +…+aqCq, где q

å ai =1 и ai Ê0.

i =1.

Тогда значение функции в точках:

F(Х) = F(a1C1 +a2C2 +…+aqCq) = a1 F(Х1) + + a2 F(Х2) + …+

+aq F(Хq) = (a1 +a2 +…+aq) М = М.

Пусть область не ограничена. Введём дополнительное ограничение:

C1 +C2 +…+CпÍS, где S-достаточно большое число.

Пусть теперь S1,S2,…,Sk –какие-то новые крайние точки, и пусть функция F достигает максимума в одной из них. Тогда максимальное значение зависит от S, поэтому S можно изменять, тем самым увеличивая максимум и делая функцию неограниченной.

Вывод. 1.ОДР-выпуклый многогранник.

2. Максимум достигается либо в одной крайней точке, либо в линейной комбинации.

Геометрическая интерпретация задачи.

Определение. Градиентом функции f (Х1, Х2, …, Хn.) в точке

0 0 0

Х0= (Х1, Х2,…,Хn) называют вектор

Ñ f (Х0) = ¶ f(Х0) ¶ f(Х0) ¶ f(Х0)

¶ f(Х1), ¶ f(Х2), ¶ f(Хп)

Градиент всегда перпендикулярен касательной к функции и направлен в сторону возрастания функции.

Рассмотрим функцию L: Ñ L=(C1, C2, …, Cn).

L (Х1,Х 2) = C1 Х1+ C2Х 2 max, C1, C2 É 0.

a11Х1+a12Х2 Í b1;

a21Х1+a22Х2 Í b2;

……………………

am1Х1+am2Х2 Í bm;

Х1,Х2 Ê 0;

max Происходит перемещение

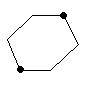опорная

прямая рисунок 1.

Происходит перемещение опорной прямой к максимуму функции.

Геометрическая интерпретация доказанных свойств.

Пусть дана функция f (Х1, Х2, …, Хn.) Её градиент:

Ñ f (Х1, Х2, …, Хn.) = ¶ f (Х1, Х2, …, Хn.) ¶ f(Х1, Х2, …, Хn.)

¶ Х1, ¶ Х2, …,

,…, ¶ f(Х1, Х2, …, Хn.)

¶ Хп.

Вернёмся к задаче f (Х1, Х2, …, Хn.) == åCi Хi max и ограничениям (2).

Ñ f (Х1, Х2, …, Хn.) = (C1, C2, …, Cn).

f (Х1,Х 2) = C1 Х1+ C2Х 2= 0. Откуда Х 2 = - C1 Х1,

C2

Функция возрастает при перемещении основной прямой в направлении градиента функции (см. рис.1).

Если область не ограничена, то задача не имеет оптимального решения.

На геометрической интерпретации основан графический метод решения задачи. Он применяется, когда n=2,3.

Вернёмся к постановке задачи линейного программирования в стандартной форме

f (Х1,Х 2) = C1 Х1+ C2Х 2 max,

a11Х1+a12Х2+…+a1nХn Í b1;

a21Х1+a22Х2+…+a2nХn Í b2;

……………………………..

am1Х1+am2Х2+…+amnХn Í bm;

Х1,Х2,…,Хn Ê 0;

Дата добавления: 2014-01-07