Теорема о крайней точке

Неравенство временно превращается в равенство и вычисляются Х1 и Х 2. Эти точки наносятся на график и строятся соответствующие ограничивающие линии. Получается некая область. Далее перемещают опорную прямую по направлению градиента функции до пересечения этой прямой с самой крайней (верхней) точкой области. Х1 и Х 2, являющиеся координатами этой точки, и являются оптимальными значениями. Но полученные значения не точны.Чтобы получить точные значения, необходимо приравнять выражения, соответствующие двум прямым, на которых располагается полученная точка. Если прямая совпадает с гранью, то можно взять любую точку, принадлежащую этой грани.

Х2) = C1 Х1 + C2Х2 max, где C1, C2 É0

Лекция 5. Основная задача линейного программирования.

Большинство алгоритмов задачи линейного программирования основаны на основной задаче линейного программирования.

Постановка задачи:

(2)

Любая задача линейного программирования, записанная в другой форме отличной от представленной (канонической), может быть сведена к основной задаче линейного программирования: max f(x)=min (-f(x)).

Если в системе ограничений содержится неравенство (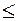или 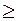), нужно перейти

к (=):

если

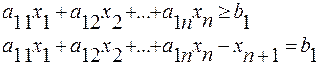
Таким образом, эти две задачи эквивалентны, т.е. задача поставлена в стандартной постановке, эквивалентна основной задаче линейного программирования с точностью до размерности. Следовательно, все свойства задачи поставленной в стандартной форме справедливы и для основной задачи линейного программирования.

Вопрос: имеет ли решение эта задача зависит от системы (2). Т.е. совместима система или противоречива.

1.Система совместима, если ранг системы, образованными коэффициентами левой части равны рангу расширенной системы.

В нашей системе ранг - r < m. Если в системе уравнений (2) m=n, то система (если она противоречива) имеет единственное решение. Если это решение положительно х>0, то это решение будет оптимальным.

Поэтому мы будем рассматривать случай, когда число ограничений m<n и будем предполагать, что все уравнения системы ограничений линейно-независимы (ни одно выражение не может быть выражено линейной комбинацией другого).

Если r=m, то система имеет бесконечное множество решений. Если не отрицательных решений нет, то основная задача не имеет допустимого решения, а так же оптимального. Если есть не отрицательные, то нам нужно из этих всех решений найти оптимальное, т.е. то, при котором функция минимальна.

2.Система противоречива.

В системе уравнений m переменных, где m=n-r. Эти переменные через которые выражается m называются свободными переменными, а m переменные называют базисными.

Выразим m переменные через n-r. Пусть это будут первые переменные:

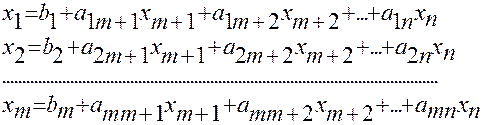(3)

путем преобразования системы (2).

Набор 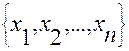называют базисом системы. Выразим 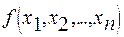через свободные переменные, получится:

Если подставить в (3) вместо свободных какие-то другие, то будем получать значение базисных переменных.

В качестве базисных переменных можно выбрать любые n-переменных из свободного числа m-переменных. Общее число базисных решений будет равно числу сочетаний:

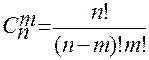
Нас интересуют положительные базисные решения, которые называются допустимыми базисными решениями. Может оказаться, что все b=0, то такое решение называется вырожденным.

Нужно найти оптимальное решение, т.о. намечается подход к решению задачи - найти допустимые базисные решения, затем перебрать их и то при котором функция будет минимальна и будет оптимальным. Таким образом, нужно перебрать все допустимые базисные решения.

Геометрическая интерпретация основной задачи линейного программирования.

Число переменных в задачи на 2 или 3 больше числа ограничений, т.е. n-m =2(3)

2-на плоскости, 3-в пространстве.

Рассмотрим когда n-m=2. Выберем в качестве свободных переменных х1,х2. Тогда остальные будут базисные. Тогда можно записать:

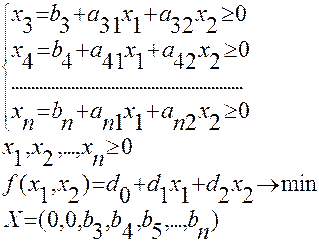
Построив график находим x1 и x2-оптимальные.

Лекция 6. СВЯЗЬ МЕЖДУ КРАЙНИМИ ТОЧКАМИ ОДР И ДОПУСТИМЫМИ БАЗИСНЫМИ РЕШЕНИЯМИ

Основная задача.

F=CX —> min

A₁X₁+A₂X₂+...+A_nX_n=A₀ (*)

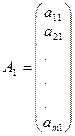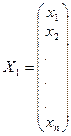, , , , C=(c₁, c₂,..., c_n)

Система векторов является линейнозависимой, если существуют числа

a₁, a₂,..., a_ь

не все =0, при которых имеет место равенство

a₁A₁+a₂A₂+... +a_mA_m=0 (1)

Если соотношение (1) возможно лишь тогда когда все a=0.

Если в системе ограничений вектора А₁,А_2,...,А_m (m<n) линейнонезависимы и существует Х_j³0 такое, что

A₁x₁+A₂x₂+...+A_mx_m=A₀,

то точка является крайней точкой области допустимых решений задачи линейного программирования.

Дата добавления: 2014-01-07