
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Пусть Х – допустимое базисное решение (*), и эта точка не является крайней
|
|
|
|
Пусть Х – допустимое базисное решение (*), и эта точка не является крайней. Пусть имеется две точки ,
,  ,
,
которые удовлетворяют системе величин


Если точка Х не крайняя, то её можно представить в виде линейной комбинации
X=lX1+(1-l)X2, 0£l£1
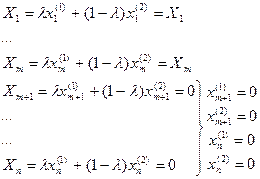
Получим
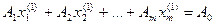
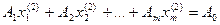
Вычтем
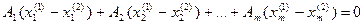
Данное равенство справедливо при
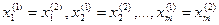
Отсюда вытекает, что точки Х1 и Х2 совпадают, а это противоречит тому что Х не является крайней точкой ==> Х – крайняя точка.
Используя теорему, о том что max целевой функции достигается если задача имеет оптимальное решение, то оно обязательно совпадает с каким либо допустимым базисным решением. Поэтому необходимо перебрать все допустимые базисные решения и выбрать то, в котором целевая функция является экстремумом. На этом основан симплексный метод решения задач линейного программирования.
Табличный алгоритм замены переменных.
Процедура перехода от одного базисного решения к другому может быть формализована и сведена к заполнению и преобразованию таблиц (симплексные таблицы). Алгоритм преобразования называется табличным алгоритмом замены переменной.
Задача в стандартной постановке:
(1) F(x1,x2,…,xn)=c1x1+c2x2+…cnxn ®max
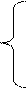 a11x1+a12x2+…+a1sxs+…a1nxn<=b1
a11x1+a12x2+…+a1sxs+…a1nxn<=b1
ai1x1+ai2x2+…+aisxs+…ainxn<=bi (2)
……..
……..
am1x1+am2x2+…+amsxs+…amnxn<=bm
xj >=0, j=1..n
Сведем эту стандартную постановку к основной задаче линейного программирования, т.е. необходимо, чтобы f®min.
F(x1,x2,…,xn)=c1x1-c2x2-…-cnxn ®min (3)
Введем дополнительные неотрицательные переменные: y1,y2,…,ym>=0, т.о. к (2) прибавляем:
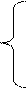 a11x1+a12x2+…+a1sxs+…a1nxn+ y1<=b1
a11x1+a12x2+…+a1sxs+…a1nxn+ y1<=b1
ai1x1+ai2x2+…+aisxs+…ainxn+ yi<=bi (4)
……..
……..
am1x1+am2x2+…+amsxs+…amnxn+ ym<=bm
xj >=0, j=1..n
Выберем в качестве базисных переменных y1,y2,…,ym , тогда все остальные будут свободными (x1,x2,…,xn). Выразим и запишем в стандартном виде:
F(x1,x2,…,xn)= 0-(c1x1+c2x2+…cnxn)®min (5)
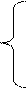 y1= b1-(a11x1+a12x2+…+a1sxs+…a1nxn)
y1= b1-(a11x1+a12x2+…+a1sxs+…a1nxn)
yi=bi-(ai1x1+ai2x2+…+aisxs+…ainxn) (6)
……..
……..
ym=bm-(am1x1+am2x2+…+amsxs+…amnxn)
Занесем полученное в таблицу:
 Базисные переменные Базисные переменные
| Свободные члены | Свободные переменные | |||||
| x1 | x2 | … | xs | … | xn | ||
    y1 y1
| b1 | a11 | a12 | … | a1s | … | a1n |
  : :
| … | … | … | … | … | … | … |
  yi yi
| bi | ai1 | ai2 | … | ais | … | ain |
   : :
| … | … | … | … | … | … | |
  yr yr
| br | ar1 | ar2 | … | ars | … | arn |
   : :
| … | … | … | … | … | … | … |
    ym ym
| bm | am1 | am2 | … | ams | … | amn |
   f f
| C0 | C1 | C2 | … | Cs | … | Cn |
 Другими словами выразить переменную yr через базисную переменную xs. Мы хотим получить: (y1,y2,…,yr,…,ym,0,…0)
Другими словами выразить переменную yr через базисную переменную xs. Мы хотим получить: (y1,y2,…,yr,…,ym,0,…0)
меняем местами
(y1,y2,…,xs,…,ym,0,…0)
Каждый разделим на ars и получим:
xs= br/ ars+(ar1*x1/ ars+ ars*x2/ ars+…+ 1*yr/ ars+…+ arn*xn/ ars)
yi= bi –(ai1*x1+ai2*x2 +…+ais*[br/ars–(ari*x1+ ars*x2/ars+ 1*yr/ars+…+arn*xn/ars)]+…+ ain*xn)= bi- ais*br/ars-((ai1- ais*ari/ars)*x1+((ai2-ais*ars/ars)*x2+ais*yr/ars+…+(ain- ais*arn/ars)*xn
Аналогично можно записать: C0=C0-bri/ars;C*s= -Cs/ars;C*j=C0-arj/ars;
Полученные значения для xs,yi и функции определяют правила преобразования таблицы при переходе от одного базисного решения к другому, т.е. при замене yr на xs.
Алгоритм замены переменных.
Строка таблицы, соответствующая переменной yr называется разрешающей строкой и помечается «®», а столбец таблицы, соответствующий переменной xs называется разрешающим столбцом и помечается «¯». Элемент таблицы, расположенный на пересечении разрешающих строки и столбца называется разрешающим элементом ars.
1) Новое значение разрешающего элемента: a*rs=1/ars
2) Новое значение элементов разрешающей строки: a*rj= a*rj/ars (i<>r)
3) Новое значение элементов разрешающего столбца получается делением старого значения на разрешающий элемент и все берется с обратным знаком a*is=-ais/ars (i<>r)
4) Все остальные элементы таблицы, не принадлежащие пунктам 1)-3), получаются как алгебраическая сумма прежнего значения и произведения элементов со значениями arj и a*is (i<>r,j<>s). a*ij=aij+arj+a*is
5) Переход к следующей таблице, в которой вместо базисной переменной yr записываем xs , а в столбце свободных переменных вместо xs записываем yr и переписываем числа из нижних частей предыдущей таблицы в верхнюю часть новой таблицы.
Лекция 7. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ Л.П.
Идея: в основе симплекс метода лежит процедура целенаправленного перебора допустимых базисных решений. Симплексный метод представляет собой вычислительный алгоритм, состоящий из конечного числа итераций. На каждой итерации находится базисное решение. В общем случае количество итераций заключено между m и 2m (m – число ограничений).
Предположим k – количество свободных переменных, n – общее количество переменных, m – количество уравнений, k=n-m.
x , x
, x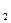 ,…, x
,…, x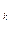 - свободные переменные.
- свободные переменные.
Выразим базисные переменные через свободные:
x = a
= a x
x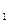 +a
+a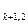 x
x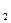 +…+a
+…+a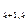 x
x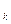 +b
+b ;
;
x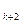 = a
= a x
x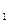 +a
+a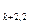 x
x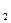 +…+a
+…+a x
x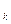 +b
+b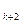 ;
;
x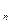 = a
= a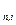 x
x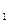 +a
+a x
x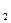 +…+a
+…+a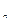 x
x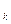 +b
+b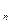 ;
;
C = j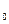 +j
+j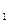 x
x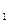 +j2x2+…+jkxk
+j2x2+…+jkxk
Из задачи геометрической интерпретации следует, что оптимальное решение находится в одной из вершин многоугольника, но в каждой из вершин k- переменных.
В частности, для k=2, вершина многоугольника – есть пересечение двух прямых, на каждой из которых соответ-я переменная равная нулю. Для попадания в первую вершину многоугольника k переменных x1,x2,…,xk
Тогда целевая функция = j0, а оставшиеся базисные переменные соответственно равны:
Xk+1=bk+1 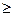 0
0
Xk+2=bk+2 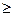 0
0
….
Xn=bn 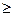 0
0
Справедливо при условии C = j0.
Целью решения задачи является минимизация задачи С. Измененные значения С получается при изменении переменных x1, x2, …, xk. Если все коэффициенты j1, j2, …, jk > 0, то при положительном изменении свободных переменных, целевая функция возрастает. Следовательно не отрицательность коэффициентов j целевой функции является признаком оптимальности полученного решения.
Предположим, что один из коэффициентов, пусть j1 < 0. Тогда, возрастание x1 приводит к уменьшению целевой функции С. Необходимо определить граничное значение переменной x1. Для этого анализируются знаки коэффициентов a , a
, a , …, a
, …, a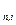 , при переменной x1. Если все коэффициенты не отрицательные, то это указывает на то, что целевая функция не ограничена на области ОДР и следовательно оптимального решения не существует.
, при переменной x1. Если все коэффициенты не отрицательные, то это указывает на то, что целевая функция не ограничена на области ОДР и следовательно оптимального решения не существует.
Предположим, что один из коэффициентов (a <0). Тогда возрастание x1 приводит к уменьшению значения xk+2. Предельное значение переменной x1 определяется нулевым значением xk+2. Следовательно, предельное значение x1 находится из ak+2,1x1 + bk+2 = 0;
<0). Тогда возрастание x1 приводит к уменьшению значения xk+2. Предельное значение переменной x1 определяется нулевым значением xk+2. Следовательно, предельное значение x1 находится из ak+2,1x1 + bk+2 = 0;
X1 = - bk+2/ ak+2,1
ak+2,1 < 0.
Таким образом, переменная xk+2=0, а x1 присвоено положительное значение. Общее количество нулевых переменных осталось неизменным, равным k, т.е. произошел переход из одной вершины многоугольника в другую. Целевая функция уменьшилась на величину j1 * (-bk+2/ ak+2,1).
Предположим, что не один, а несколько коэффициентов при x1 отрицательны. Тогда предельное значение x1 будет определяться из:
x1 = min {- bk+i/ak-i,1} при условии ak-i,1<0.
Описанная процедура повторяется пока, все коэффициенты j целевой функции не станут неотрицательными. Перед выполнением процедуры необходимо выполнить преобразования связанные с переводом xi с правой части уравнения в левую часть и наоборот xk+i из левой части в правую.
Лекция 8. Алгоритм нахождения допустимого базисного значения.
1)Исходная задача сводится к основной задаче линейного программирования.
2)Задача записывается в стандартной записи.
3)Заполняется симплексная таблица, коэффициенты которой переносятся из стандартной записи задачи.
4)Анализ свободных членов симплексной таблицы. Если все элементы столбца свободных членов (кроме последнего) неотрицательны,то получено ДБР. Базисные переменные равны соответствующим свободным членам, а все свободные переменные равны 0.
Переход к поиску оптимального решения.
5)Анализ задачи на разрешение. Если в симплексной таблице найдётся строка в которой свободный член отрицательный,а все элементы этой строки неотрицательны, то задача не имеет решения.
6)Выбор разрешающего столбца.В строке с отрицательным свободным членом выбирается любой отрицательный элемент и столбец,в котором расположен этот элемент объявляется разрешающим.
7)Выбор разрешающей строки.
Для элементов разрешающего столбца,вычисляется (если существуют симплексные отношения). Строка для которой симплексные отношения min объявляется разрешающей строкой. Если min симплексные отношения не единственные, то выбирается любая строка в качестве разрешающей строки.
8)Используя табличный алгоритм замены переменных, преобразуем симплексную таблицу. Меняем местами переменные соответствующие разрешающей строки и столбца. Переход на п.4 алгоритма.
Нахождение оптимального решения.
1) Пусть в результате проведения к итерации над симплексной таблицей получено ДБР. Из числа базисных переменных выведены 1-е переменные у1…ук, а введены переменные х1….хк. Обозначим элементы строки целевой функции С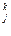 (j=
(j=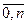 ).Пусть какой-то элемент С
).Пусть какой-то элемент С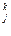 >0, а элементы этого столбца a
>0, а элементы этого столбца a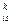 , а все элементы этого столбца отрицательны (i=
, а все элементы этого столбца отрицательны (i=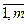 ).Тогда для какого-то i-го элемента строки Хi =bi -(Y
).Тогда для какого-то i-го элемента строки Хi =bi -(Y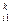 *Y1 +X
*Y1 +X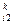 *Y2 +…+X
*Y2 +…+X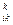 *Yk + …+
*Yk + …+ a
a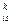 *Xs+…+ a
*Xs+…+ a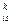 *Xn), где i<k
*Xn), где i<k
Yj=bj –(a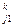 *Y1+a
*Y1+a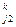 *y2 +…+a
*y2 +…+a *yk +a
*yk +a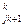 *Xk+1 +…+a
*Xk+1 +…+a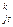 *ys +…+a
*ys +…+a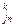 *Xn), j>k.
*Xn), j>k.
F=C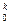 -(C
-(C +…+ C
+…+ C *Yk +…+ C
*Yk +…+ C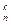 *Xn)
*Xn)
Приравняем к 0: y1=y2=…=yk=0,Xk+1=0,Xs-1=0,Xs¹0, Xs+1=0,Xn=0.
А a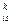 £0, a
£0, a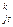 £0
£0
Пусть Xs®¥,тогда Xi, будут положительными. Если посмотреть на функцию, то видно, что она будет убывать неограниченно.Таким образом, получим критерий неограниченно. Таким образом, получим критерий неограниченности целевой функции. Если в таблице найдётся такой столбец в котором коэффициент в строке целевой функции положительный, а все элементы этого столбца £0, то целевая функция в исходной задаче неограниченна,т.е. задача не имеет оптимального решения.
2)Пусть значение целевой функции после K итераций равно С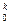 .
.
Пусть в качестве следующей итерации выполняем К+1, в качестве разрешающей строки выбрана строка r, и столбец S,разрешающий элемент a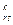 . После к+1 шага новое значение будет равно С
. После к+1 шага новое значение будет равно С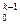 = С
= С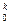 -
- . Если С
. Если С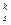 >0,то С
>0,то С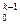 < С
< С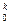 , т. е значение функции уменьшилось. Если для всех элементов строки функции S=
, т. е значение функции уменьшилось. Если для всех элементов строки функции S= С
С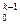 <0, то значение функции будет больше. Т.е при любом выборе разрешающего столбца уменьшение функции невозможно.
<0, то значение функции будет больше. Т.е при любом выборе разрешающего столбца уменьшение функции невозможно.
Критерий оптимальности решения:
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 598; Нарушение авторских прав?; Мы поможем в написании вашей работы!