Датчики случайных чисел

Получение и преобразование случайных чисел.

Распространены два основных способа получения случайных чисел:

1) Случайные числа вырабатываются специальной электронной приставкой (датчиком случайных чисел), устанавливаемой на ЭВМ. Реализация этого способа почти не требует дополнительных операций, кроме обращения к датчику случайных чисел.

2) Алгоритмический способ – основан на формировании случайных чисел в самой машине посредством специальной программы. Недостатком этого способа является дополнительный расход машинного времени, так как в этом случае машина выполняет операции самой электронной приставки.

Программа выработки случайных чисел заданным законом распределения может оказаться громоздкой. Поэтому случайные числа с заданным законом распределения обычно получают не непосредственно, а путем преобразования случайных чисел, имеющих какое-то стандартное распределение. Часто таким стандартным распределением является равномерное распределение (простота получения и удобство преобразования в другие законы).

Получение случайных чисел с равномерным законом наиболее выгодно получать с помощью электронной приставки, освобождающей ЭВМ от дополнительных затрат машинного времени. Получение чисто равномерного распределения на ЭВМ невозможно в силу ограниченности разрядной сетки. Поэтому вместо непрерывной совокупности чисел на интервале (0, 1) используют дискретную совокупность из 2ⁿ чисел, где n – разрядность машинного слова.

Закон распределения такой совокупности носит название квазиравномерного. При n³20 различия между равномерным и квазиравномерным законами становятся несущественными.

Для получения квазиравномерных случайных чисел используют 2 способа:

1) генерирование случайных чисел с помощью электронной приставки путем моделирования некоторых случайных процессов;

2) получение псевдослучайных чисел с помощью специальных алгоритмов.

Для получения n -значного двоичного случайного числа по первому способу моделируется последовательность независимых случайных величин z_i, принимающих значение 0 или 1. полученная последовательность 0 и 1, если рассматривать ее как дробное число, и представляет собой случайную величину квазиравномерного распределения на интервале (0, 1). Аппаратные методы получения этих чисел различаются только способом получения реализации z_i.

Один из способов основан на подсчете количества радиоактивных частиц за определенный промежуток времени Dt, если число частиц за Dt четное, то z_i = 1, а если нечетное, то z_i = 0.

Другой способ использует шумовой эффект электронной лампы. Фиксируя значение шумового напряжения в определенные моменты времени t_i, получаем значения независимых случайных величин U(t_i), т.е. напряжение (Вольт).

Величина z_i определяется по закону:

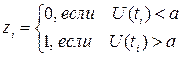
где a – некоторое значение порогового напряжения.

Величина a обычно выбирается из условия:

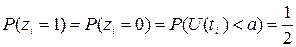
Недостаток аппаратного способа в том, что он не позволяет применять метод двойного прогона для контроля работы алгоритма решения какой – либо задачи, так как при повторном прогоне не удается получать те же случайные числа.

Псевдослучайными называют числа, сформированные на ЭВМ с помощью специальных программ рекуррентным способом: каждое случайное число получают из предыдущего с помощью специальных преобразований.

Простейшее из этих преобразований следующее. Пусть имеется некоторое n – разрядное двоичное число из интервала nÎ (0, 1). Возведем его в квадрат, при этом получим уже 2ⁿ разрядное число. Выделим средние n разрядов. Полученное таким образом n – разрядное число и будет новым значением случайного числа. Его опять возводим в квадрат и т.д. Такая последовательность псевдослучайна, т.к. с теоретической точки зрения она не является случайной.

Недостатком рекуррентных алгоритмов является то, что последовательности случайных чисел могут выродиться (например, будем получать только нулевую последовательность или последовательность единиц, или может проявляться периодичность).

Дата добавления: 2014-01-07