Получение случайных чисел с заданным законом распределения

Псевдослучайные числа могут быть использованы в качестве исходного материала для моделирования любых вероятностных объектов (случайные события и связанные с ними процессы).

Пусть, например, событие А имеет вероятность Р(А), тогда процедура его моделирования с помощью равномерно распределенных в интервале (0, 1) чисел производится так:

1) Выбирается очередное случайное число x_i.

2) Проверкой неравенства x_i £ Р(А) устанавливается принадлежность этого числа отрезку [0, Р(А)]. Если неравенство выполнено, то говорят, что событие А наступило, в противном случае – не наступило.

Аналогично выглядит процедура моделирования на ЭВМ дискретной случайной величины с заданным законом распределения:

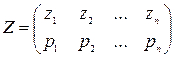
Разобьем интервал (0, 1) на n интервалов, длины которых выберем равными р₁, р₂, …, р_n.

Координаты точек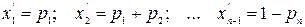

Моделирование сводится к следующему: для получения очередного значения Z вырабатывается очередное x_i и при попадании его в j -ый интервал считается, что Z приняло значение Z_j.

Все разнообразие методов получения случайных чисел можно разделить на 2 группы: точные и приближенные методы.

Пусть равномерно распределенная в интервале (0, 1) величина X получается из случайной величины Y с помощью неслучайной функции h(y), тогда очевидно неравенство:

.

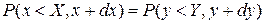Выражая левую и правую части через соответствующие плотности распределения и учитывая, что f(x)=1, получаем:

.

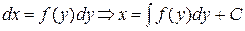Учитывая далее, что по определению 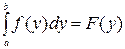, где а – произвольное число, F(y) – интегральная функция распределения случайной величины Y. Кроме того, очевидно, что F(a)=0.

Найдем окончательно вид функции h(y) = F(y), совпадающее с интегральным законом. Для получения очередного значения y_i случайной величины Y, распределенной в интервале (a, b) с законом распределения f(y) соответствующего значению x_i необходимо решить уравнение:

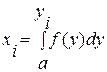(1).

Пример. Пусть необходимо получить случайные числа с последовательным законом распределения, т.е. 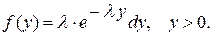используя соотношение (1), имеем:

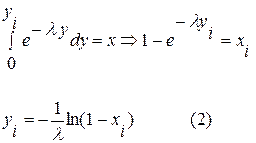
Можно привести другие примеры использования выражения (1). Однако, подобная методика находит ограниченное применение благодаря двум обстоятельствам:

1) Для многих законов распределения интеграл правой части уравнения (1) в конечном виде не берется, например, нормальный закон.

2) Даже когда интеграл (1) удается взять в конечном виде, формулы получаются слишком громоздкими, требующими больших затрат машинного времени, поэтому используют приближенные методы.

Рассмотрим один из универсальных приближенных способов.

Пусть закон распределения случайной величины Y, предложенной для моделирования, задан функцией плотности f(y), возможные значения которой в интервале (a, b). Если этот интервал с бесконечными границами, то целесообразно перейти к усеченному распределению, оставив лишь существенную часть.

Представим f(y) на участке (a, b) в виде кусочно-постоянной функции, т.е. разобьем (a, b) на n интервалов и будем считать f(y) на каждом интервале постоянной, тогда случайную величину Y можно представить в виде: Y=a_k + X_k, т.е. на каждом участке (a_k, a_k+1) величина X_k считается распределенной равномерно (см. рисунок).

Чтобы аппроксимировать f(y) наиболее удобным способом целесообразно разбить (a, b) на интервалы таким образом, чтобы вероятность попадания случайной величины Y в любой интервал (a_k, a_k+1) была постоянной, т.е. не зависела от номера интервала k. Для вычисления пользуются следующим соотношением: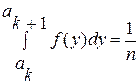, где n – количество интервалов обычно принимаемое равным 2^m, где m – целое положительное число.

Процедура моделирования предполагает следующее:

1) Выбирается случайное равномерно распределенное число x_i.

2) С помощью x_i выбирается интервал (a_k, a_k+1).

3) Берется следующее равномерно распределенное число x_i+1 и масштабируется с целью приведения к интервалу (a_k, a_k+1), т.е. x_i+1 становится случайной величиной, равномерно распределенной в интервале (a_k, a_k+1). Случайное число y_i с требуемым законом распределения находится по формуле: y_i = a_k + x_i+1 (a_k+1 - a_k).

Рассмотрим процесс выборки интервала (a_k+1 - a_k) с помощью x_i. Случайное число x_i получается на ЭВМ в виде последовательности 0 и 1. Если m – разрядность двоичного числа, то всего чисел будет 2^m и каждому интервалу (a_k+1 - a_k) можно поставить в соответствие только одно двоичное число, что значительно упрощает процедуру выбора интервала (a_k+1 - a_k).

Для реализации данного метода на ЭВМ требуется небольшое количество операций, причем число операций не зависит от точности аппроксимации, т.е. от количества интервалов n. Точность аппроксимации (количество n) влияет только на размеры участка памяти, куда помещается таблица закодированных значений a_k. Этот способ находит широкое распространение в практике имитационного моделирования.

Метод Неймана (разыгрывания случайной величины)

Д. Нейман предложил способ получения заданного закона распределения, не требующий решения интегрального уравнения (1) и в то же время являющийся точным, т.е. не использующим никаких приближений.

Метод основан на имитационном моделировании закона распределения. Суть его сводится к следующему.

Пусть X распределена на интервале (a, b) и моделируемая плотность ограничена: f(x)£M₀. Выбираем два значения g₁ и g₂, равномерно распределенных в интервале (0, 1) случайной величины g и на плоскость (x, f(x)) наложим точку N с координатами: a=a + g₁ (b-a); b=g₂ M₀.

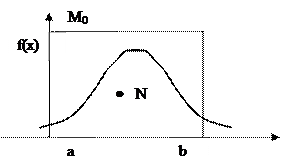Если точка N лежит под кривой, то разыгранное полученное значение X считается равным a. Если точка оказалась под кривой, то пару g₁, g₂ отбрасывают и выбирают новую пару g₃ и g₄.

Покажем, что указанный алгоритм приводит к закону f(x). Случайная точка N равномерно распределена в прямоугольнике с площадью (b-a)´M₀.

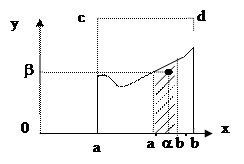Вероятность того, что точка N окажется ниже прямой f(x) равна отношению:

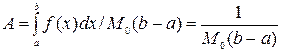
Вероятность того, что точка окажется под кривой f(a) и окажется внутри интервала (a’, b’) выражается соотношением:

.

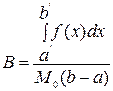Следовательно, среди всех отобранных (перешедших в X) a доля попавших в интервал (a’, b’) равна частному:

.

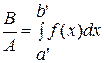Если же вероятность того, что P(a’ £ X £ b’) находится через плотность f(x), то это значит, что X имеет плотность f(x).

Дата добавления: 2014-01-07