Критерий Михайлова

Частотные критерии устойчивости

Критерий Михайлова сформулирован и обоснован в 1936 году русским ученым А.В. Михайловым. Критерий Михайлова позволяет оценивать устойчивость как замкнутых, так и разомкнутых систем.

Пусть характеристический полином системы имеет вид:

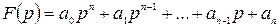. (4.9)

Заменив p на jw, получим, что

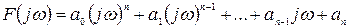. (4.10)

Тогда можно записать, что

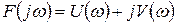, (4.11)

где 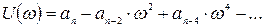, т.е. содержит только четные степени w; 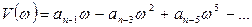, т.е. содержит только нечетные степени w;

При изменении частоты w от 0 до +¥ конец вектора F(jw) опишет некоторую линию, называемую годографом Михайлова.

Критерий Михайлова. Система, описываемая характеристическим уравнением п -го порядка устойчива, если при изменении частоты w от 0 до +¥ годограф Михайлова повернется в положительном направлении (против часовой стрелки), начиная с вещественной положительной полуоси на число квадрантов, равное порядку характеристического уравнения, т.е. на угол 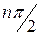, нигде не обращаясь в нуль. Для устойчивой системы при п =4 годограф Михайлова приведен на рис. 4.2, для системы на границе устойчивости на рис. 4.3.

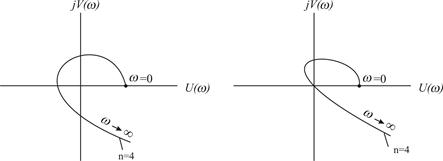
Рис. 4.2. Система устойчива Рис. 4.3. Система на границе устойчивости

Таким образом, если система находится на границе устойчивости, то годограф Михайлова проходит через начало координат.

Система неустойчива по критерию Михайлова, если годограф Михайлова проходит п квадрантов непоследовательно или проходит меньшее число квадрантов. Годографы Михайлова для неустойчивых систем при п =4 приведены на рис. 4.4.

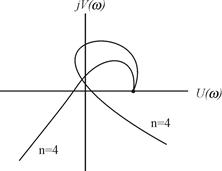
Рис. 4.4. Годографы Михайлова для неустойчивых систем

Следствие из критерия устойчивости Михайлова: Система устойчива, если действительная и мнимая части характеристического полинома F(jw) обращаются в нуль поочередно, как показано на рис. 4.5, т.е. если корни уравнений U(w) =0 и V(w) =0 перемежаются.

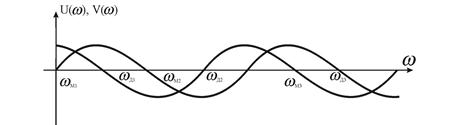
Рис. 4.5. Графики U(w) и V(w)

Критерий Михайлова удобно применять для оценки устойчивости систем высокого порядка (n³4).

Дата добавления: 2014-01-07