Критерий Найквиста

Критерий устойчивости Найквиста сформулирован и обоснован в 1932 году американским физиком Х. Найквистом. Критерий устойчивости Найквиста наиболее широко используется в инженерной практике по следующим причинам:

- устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой части W_p(jw), а эта функция, чаще всего, состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости;

- для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объекта управления, исполнительных органов), что повышает точность полученных результатов;

- устойчивость системы можно исследовать по логарифмическим частотным характеристикам, построение которых не сложно;

- достаточно просто определяются запасы устойчивости системы;

- удобно использовать для оценки устойчивости САР с запаздыванием.

Критерий устойчивости Найквиста дает возможность оценивать устойчивость САР по АФЧХ ее разомкнутой части. При этом различают три случая применения критерия Найквиста.

1.Разомкнутая часть САР устойчива. Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой части системы (годограф Найквиста) при изменении частоты w от 0 до +¥ не охватывала точку с координатами [-1, j 0]. На рис. 4.6 приведены основные возможные ситуации:

1. - замкнутая система абсолютно устойчива;

2. - САР условно устойчива, т.е. устойчива только в некотором диапазоне изменения коэффициента передачи k;

3. - САР находится на границе устойчивости;

4. - САР неустойчива.

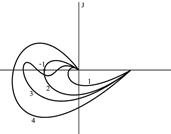
Рис. 4.6. Годографы Найквиста, когда разомкнутая часть САР устойчива

2. Разомкнутая часть САР находится на границе устойчивости. В этом случае, характеристическое уравнение имеет нулевые или чисто мнимые корни, а у остальных корней вещественные части отрицательны.

Для устойчивости замкнутой системы, если разомкнутая часть системы находится на границе устойчивости необходимо и достаточно, чтобы АФЧХ разомкнутой части системы при изменении w от 0 до +¥, дополненная на участке разрыва дугой бесконечно большого радиуса не охватывала точку с координатами [-1, j 0]. При наличии ν нулевых корней АФЧХ разомкнутой части системы при w =0 дугой бесконечно большого радиуса перемещается от положительной вещественной полуоси на угол 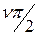градусов по часовой стрелке, как показано на рис. 4.7.

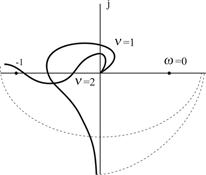
Рис. 4.7. Годографы Найквиста при наличии нулевых корней

Если имеется пара чисто мнимых корней w_i=, то АФЧХ при частоте w_i дугой бесконечно большого радиуса перемещается на угол 180° по часовой стрелке, что отражено на рис. 4.8.

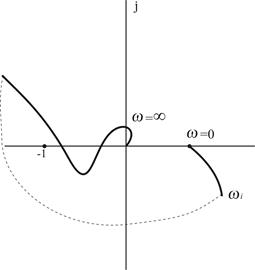
Рис. 4.8. Годограф Найквиста при наличии пары чисто мнимых корней

3. Разомкнутая часть системы неустойчива, т.е. характеристическое уравнение имеет l корней с положительной вещественной частью. В этом случае, для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты w от 0 до +¥ АФЧХ разомкнутой части САР охватывала точку

[-1, j 0) l /2 раз в положительном направлении (против часовой стрелки).

При сложной форме годографа Найквиста удобнее применять другую формулировку критерия Найквиста, предложенную Я.З. Цыпкиным, используя правила переходов. Переход АФЧХ разомкнутой части системы при увеличении w отрезок вещественной оси от -1 до -¥ сверху вниз считается положительным (рис. 4.9), а снизу вверх отрицательным. Если АФЧХ начинается на данном отрезке при w =0 или заканчивается при w =¥, то считается, что АФЧХ совершает пол перехода.

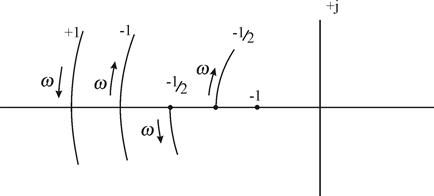
Рис. 4.9. Переходы годографа Найквиста через отрезок P(w) от -¥ до -1

Замкнутая система устойчива, если разность между числом положительных и отрицательных переходов годографа Найквиста через отрезок вещественной оси от -1 до -¥ равно l/2, где l – число корней характеристического уравнения с положительной вещественной частью.

Дата добавления: 2014-01-07