Функция распределения молекул идеального газа по скоростям

(распределение Максвелла)

Согласно модели идеального газа средняя кинетическая энергия молекул прямо пропорциональна его абсолютной температуре:

. (4.8)

Рассчитаем средне квадратичную скорость молекул воздуха при :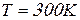

.

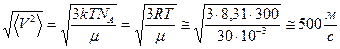При той же температуре скорость молекулы водорода 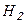, масса которой значительно меньше массы молекулы воздуха (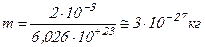), равна:

.

Из приведенных чисел видно, что молекулы окружающего нас воздуха движутся со скоростями порядка скорости полета пуль. Экспериментально скорости теплового движения молекул были определены Штерном. Схема опыта Штерна изображена на Рис.6.

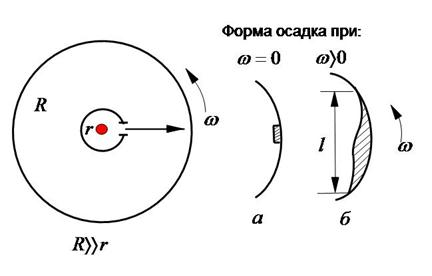
Два коаксиальных цилиндра, радиусы которых связаны соотношением 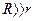, по оси расположена платиновая проволока, покрытая слоем серебра и нагреваемая электрическим током. Температуру проволоки можно измерить по её электрическому сопротивлению. Серебро одноатомно, т.е. его молекулы идентичны с атомами. При температуре атомы серебра испаряются с поверхности проволоки и разлетаются во все стороны со скоростями, которые можно рассчитать по уравнению (4.8). В системе создавали вакуум, чтобы летящие атомы серебра не испытывали на своем пути столкновений с молекулами воздуха. Через узкую щель вдоль внутреннего цилиндра вылетает пучок атомов серебра, скорости которых направлены вдоль радиусов цилиндров. Долетая до холодной стенки внешнего цилиндра, атомы серебра осаждаются, образуя серебреную полоску – изображение щели внутреннего цилиндра. Если цилиндры привести во вращении, то форма осадка на внешнем цилиндре изменяется. Пока атом серебра, летящий со скоростью 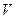, проходит расстояние между цилиндрами , цилиндры успевают повернуться на угол 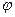. Вспомнив соотношение между дугой и центральным углом 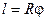и между линейной и угловой скоростью 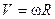, получим выражение для скорости молекул серебра, долетающих до внешнего цилиндра:

отсюда имеем для скорости молекул серебра

. (4.9)

Форма осадка показывает, что молекулы серебра имеют различные скорости. Причем одни скорости встречаются чаще, а другие реже. Кроме того, исходя из данных эксперимента,

была рассчитана скорость молекул серебра. Результаты расчетов подтвердили справедливость уравнения (4.8).

Математическое выражение функции распределения по скоростям молекул идеального газа при тепловом равновесии было впервые получены Максвеллом в 1860 г. Ввиду полной беспорядочности движения молекул, нельзя ставить вопроса о числе молекул которые обладают точно заданной скоростью 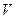. Таких молекул в каждый данный момент вообще может не оказаться. Но можно поставить вопрос о числе молекул, скорости которых лежат в некотором определенном интервале скоростей. Максвелл, пользуясь теорией вероятности, подсчитал число молекул (), скорости которых лежат в интервале скоростей от некоторой скорости (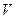) до (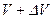), введя коэффициент пропорциональности, который зависит от скорости - функцию распределения молекул идеального газа по скоростям:

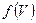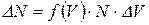(4.10)

Из уравнения (4.11) можно выразить долю молекул попадающих в заданный интервал вблизи некоторой скорости, т.е. вероятность попадания молекул в заданный интервал:

(4.11)

Из уравнения (4.12) выразим функцию распределения молекул идеального газа по скоростям – функцию Максвелла:

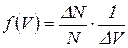(4.12)

Таким образом, функция Максвелла определяет долю молекул, попадающих единичный интервал скоростей вблизи определенной скорости, т.е. плотность вероятности.

Запишем конкретное уравнение функции Максвелла:

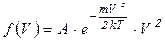, (4.13)

где 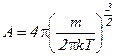- коэффициент, независящий от скорости.

Функция распределения молекул по скоростям представлена на Рис.7.

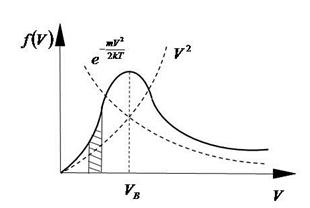
Вероятность попадания молекул в заданный интервал, т.е. 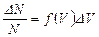, на графике функции Максвелла выражается заштрихованной площадью. Очевидно, что вся площадь под графиком дает вероятность попадания молекул газа в интервал скоростей от нуля до бесконечности.

Эта функция стремится к нулю при скоростях 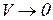и . Следовательно, относительное число молекул в газе, обладающих как очень, малыми так и очень большими скоростями, ничтожно мало. При некоторых скоростях функция имеет максимум, т.е. молекулы со скоростями, близкими к скоростям, определяющим положение максимума, встречаются очень часто. Скорость, при которой функция Максвелла достигает максимума, называется вероятной скоростью. Определим значение вероятной скорости, взяв производную функции распределения по скорости и приравняв её к нулю:

,

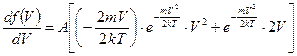если 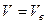, тогда .

Рассчитаем значение вероятной скорости, подставив 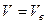в уравнение производной:

.

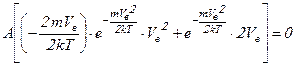Следовательно, 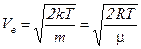(4.14)

. Подставим значение вероятной скорости в функцию распределения и выясним, как ведет себя максимум функции Максвелла:

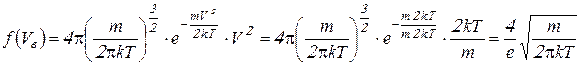
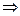
(4.15)

Таким образом, при возрастании температуры вероятная скорость увеличивается (максимум функции распределения сдвигается вправо), а плотность вероятности (высота максимума функции) уменьшается. При этом число медленных молекул (малые скорости) убывает, а число быстрых возрастает. При этом площадь под графиком, т.е. вероятность попадания молекул в интервал скоростей от нуля до бесконечности, всегда остается постоянной и равна единице, т.к. это событие достоверное, которое наверняка произойдет:

(4.16)

Уравнение (4.16) называется условием нормировки, а функция Максвелла – функция нормированная. На Рис.8 представлены функции распределения для двух температур.

Функция Максвелла позволяет, помимо вероятной скорости 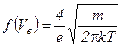, определить средне квадратичную и средне арифметическую скорости:

; (4.17)

Дата добавления: 2014-01-07