Применение первого начала для изороцессов

Из уравнения (5.12) следует, что на круговом процессе система не может совершать работу без подвода извне тепла или совершать работу, большую, чем подводимое извне тепло. Другими словами. невозможно создать вечный двигатель первого рода.

Первое начало термодинамики является выражением одного из основных законов природы – закона сохранения и превращения энергии. Формулировок первого начала несколько. Приведем некоторые из них.

Первое начало термодинамики

Для круговых процессов. Опыт показывает, что отношение тепла, полученного системой, к работе, совершенной системой при круговом процессе, одинаково для всех систем и для всех круговых процессов:

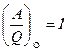следовательно, . (5.12)

Для некруговых процессов. Рассмотрим два произвольных некруговых процесса 1а2 и 1в2 (Рис.3);

Дополним эти процессы до круговых, введя участок 2с1. Теперь можно рассмотреть два произвольных круговых процесса и записать для каждого уравнение первого начала термодинамики:

; .

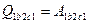Вычтя из первого уравнения второе, получим:

или, если исключить из рассмотрения ветвь 2с1, получим:

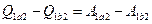, следовательно, окончательно имеем:

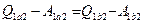. (5.13)

Таким образом, разность между теплотой, подведенной к системе, и работой, которую совершила система, не зависит от пути перехода системы из состояния 1 в состояние 2; она зависит лишь от начального и конечного состояния. Величина есть мера изменения некоторой физической величины, являющейся функцией изменения состояния. Ранее было показано, что внутренняя энергия идеального газа зависит лишь от температуры, следовательно, её изменение будет определяться лишь изменением состояния газа. Следовательно, .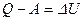

Окончательно запишем и сформулируем первое начало термодинамики в интегральной форме.

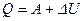(5.14)

Все подведенное к системе тепло расходуется на работу, совершаемую системой, и на изменение её внутренней энергии.

Выражение (5.14) удобнее записывать для малого изменения состояния системы, вызванного сообщением ей малого количества теплоты и совершением системой элементарной работы , т.е. в дифференциальном виде:

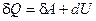(5.15)

Различие в записи малого приращения внутренней энергии 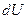и элементарного количества тепла , а также элементарной работы имеет глубокий физический смысл. Ранее было отмечено, что внутренняя энергия – функция состояния. Следовательно, при любом круговом процессе её изменение равно нулю, а 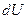представляет собой полный дифференциал.

Работа и теплота таким свойством не обладают. Поэтому величины и не являются полными дифференциалами. Эту же мысль можно выразить и так: как теплота, так и работа – характеристики процесса, внутренняя энергия – функция состояния, изменение внутренней энергии - функция изменения состояния газа.

Среди многочисленных практических применений термодинамики наиболее часто приходится иметь дело с изопроцессами. Разберем эти процессы более подробно.

Изохорический процесс ().

1. Уравнение состояния принимает вид 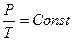, где .

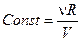2. Диаграмма в координатах имеет вид (Рис.4).

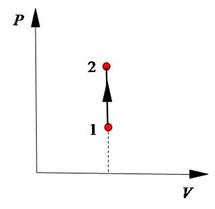
3. По этой диаграмме совершенно очевидно, что работа газа в изохорическом процессе равна нулю, так как она численно равна площади под графиком и рассчитывается по уравнению .

4. Запишем уравнение первого начала термодинамики для изохорического процесса:

в интегральном виде - ;

в дифференциальном виде - .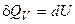

Следовательно, все, подведенное к газу тепло, идет только на изменение его внутренней энергии.

5. определим молярную теплоемкость газа при изохорическом процессе:

.

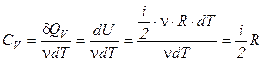Изобарический процесс. ()

1. Уравнение состояния принимает вид 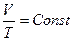, где .

2. Диаграмма в координатах имеет вид (Рис.5).

3. По этой диаграмме совершенно очевидно, что газ в изобарическом процессе совершает работу, она численно равна площади под графиком и рассчитывается по уравнению 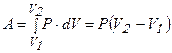, так как .

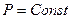4. Запишем уравнение первого начала термодинамики для изобарического процесса:

в интегральном виде - ;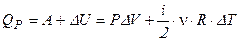

в дифференциальном виде - .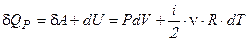

Следовательно, все, подведенное к газу тепло, идет на совершение газом работы и на изменение его внутренней энергии.

5. определим молярную теплоемкость газа при изобарическом процессе:

.

По уравнению состояния идеального газа 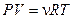при постоянном давлении получаем 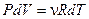. Тогда уравнение для молярной теплоемкости газа в изобарическом процессе принимает вид:

.

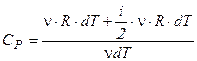Окончательно уравнение для молярной теплоемкости при изобарическом процессе в газе запишем с учетом ранее полученного уравнения для молярной теплоемкости в изохорическом процессе в виде:

или .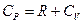

Последнее уравнение, которое связывает молярные теплоемкости при изохорическом и изобарическом процессах, называется уравнением Майера.

Изотермический процесс ().

1. Уравнение состояния принимает вид , где ;

2. Диаграмма в координатах имеет вид (Рис.6):

3. По этой диаграмме совершенно очевидно, что газ в изотермическом процессе совершает работу, так как она численно равна площади под графиком и рассчитывается по уравнению , так как ;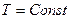

4. Запишем уравнение первого начала термодинамики для изотермического процесса:

в интегральном виде - ;

в дифференциальном виде - .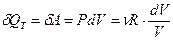

Следовательно, все, подведенное к газу тепло, идет только на совершение газом работы

5. Определим молярную теплоемкость газа при изотермическом процессе:

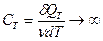
Адиабатический процесс ()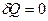

Процесс, совершаемый системой без теплообмена, т.е. когда отсутствует обмен энергией в форме теплоты между системой и внешней средой, называется адиабатическим. Он представляет большой практический интерес, так как используется в двигателях внутреннего сгорания, холодильных установках и пр. Практически адиабатический процесс осуществляется при достаточно быстром расширении или сжатии газа, когда не успевает пройти теплообмен между газом и внешней средой. Например, прокол или накачка автомобильной шины.

Первый закон термодинамики для адиабатического процесса записывается следующим образом:

, или если записать для одного моля (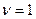), то имеем .

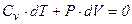Из первого начала термодинамики следует, что при адиабатическом процессе газ совершает работу за счет изменения своей внутренней энергии:

Дата добавления: 2014-01-07