Свободные незатухающие колебания

Дополнение к лекции по свободным незатухающим колебаниям.

Колебания – движения или состояния, параметры которых повторяются во времени. Колебания в той или иной мере встречаются во всех явлениях природы: от пульсации излучения звезд, движения планет до внутриклеточных процессов или колебаний атомов и молекул, колебаний полей.

В физике особо выделяют механические и электромагнитные колебания (и их комбинации).

Моделью для изучения механических колебаний является осциллятор – материальная точка или система, совершающая колебательное периодическое движение около положения устойчивого равновесия. (Более того, термин осциллятор применим к любой системе, если описывающие ее величины периодически меняются во времени.) Простейшие примеры осцилляторов – грузик на пружине, маятник.

Пример. Груз массы m подвешен на невесомой пружине жесткости k в поле сил тяжести (пружинный маятник). Найти период его колебаний. Сопротивлением воздуха пренебречь.

Решение. Запишем уравнение его движения в проекции на вертикальное направление Y

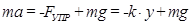или .

где y – величина растяжения пружины. Положение равновесия груза на пружине . Введем смещение груза от положения равновесия 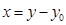, тогда , .

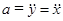Получаем уравнение , .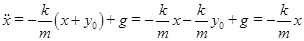

Здесь 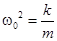и период колебаний .

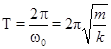Механическая энергия груза на пружине .§

Пример. Найдем период колебаний математического маятника - материальной точки массы m, подвешенной на невесомой нерастяжимой нити длины l.

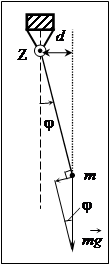Решение. Рассмотрим движение маятника в тот момент, когда он поднимается. Отклонение нити от вертикали зададим угловой координатой j. При этом если угол j увеличивается (против часовой стрелки), то касательное ускорение точки направлено против направления движения. Поэтому уравнение движения имеет вид:

.

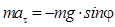Вблизи положения равновесия проекция сила тяжести должна быть представлена как квазиупругая сила. Если выполняется условие малости колебаний, то 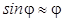, поэтому длина дуги окружности , следовательно, проекция силы тяжести . Поэтому коэффициент в выражении для квазиупругой силы 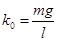. Касательное ускорение связано с угловым ускорением соотношением 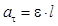(где ), поэтому, после сокращения массы m получим:

.

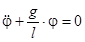С учетом выражения для циклической частоты 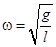период колебаний имеет вид . Механическая энергия математического маятника

.

При движении по окружности , , 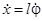поэтому

.

Дата добавления: 2014-01-15