Векторная диаграмма

Рассмотрим радиус-вектор точки М, вращающейся вокруг начала координат с угловой скоростью w. Тогда угол между радиус-вектором и осью Х меняется с течением времени по закону , где j₀ – его начальное значение. Пусть длина радиус-вектора úОМê=А

Координаты точки М:

описывают колебания осциллятора вдоль осей.

Данная форма представления колебаний называется амплитудной (векторной) диаграммой.

Рассмотрим сложение двух колебаний одного направления: два осциллятора совершают колебания вдоль оси Х с циклическими частотами w₁ и w₂

и .

Зададим эти колебания на векторной диаграмме с помощью векторов.

1-е колебание задаётся вектором , который вращается вокруг начала координат с постоянной угловой скоростью w₁, угол вращения меняется по закону .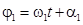

2-е колебание задаётся вектором 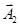, соответственно, угол .

Тогда результирующему колебанию 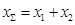сопоставим вектор с фазой

По теореме косинусов

Учтем, что ,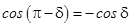

, тогда

или .

Соответственно, .

Остановимся подробнее на двух частных случаях.

1) Пусть 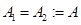, 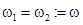. Тогда .

Амплитуда результирующего колебания в этом случае не зависит от времени.

Если разность начальных фаз колебаний , где n – целое число, то наблюдается усиление колебаний .

Если разность начальных фаз колебаний , где n – целое число, то колебания гасят друг друга .

Для вывода формулы результирующего колебания воспользуемся соотношением

, поэтому, учитывая четность функции косинус:

Амплитудой должно быть выражение не зависящее от времени, но амплитуда не может быть отрицательной величиной, следовательно

,

Тогда

.

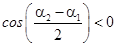Если , то , но если то .

2) Рассмотрим случай, когда амплитуды одинаковые 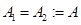, но частоты отличаются на небольшую величину 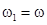, , 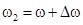. Для упрощения примем, что и . Поступая как и в предыдущем случае, получаем

.

Пренебрегая в выражении для фазы второго сомножителя величиной 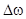по сравнению с w, получаем:

.

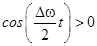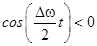Если , то , но если то .

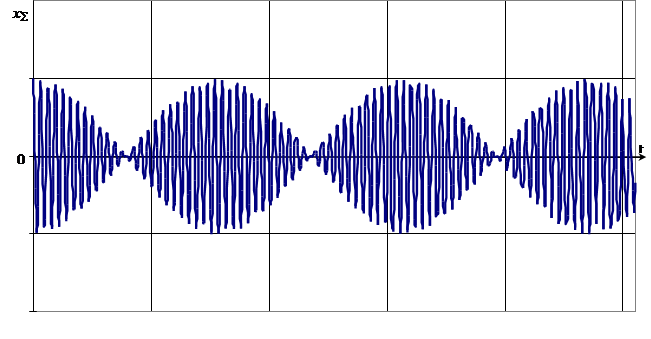
Таким образом, при сложении колебаний близких частот возникает периодическое изменение амплитуды и скачкообразное изменение фазы результирующего колебания – явление, которое называется биением.

Дата добавления: 2014-01-15