
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема (Гаусс). Якщо многочлен з цілими коефіцієнтами можна розкласти на множники з раціональними коефіцієнтами, то його можна розкласти на множники з цілими коефіцієнтами
|
|
|
|
Наслідок 1. Якщо алгебраїчне рівняння з цілими коефіцієнтами
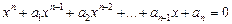
має раціональний корінь, то він є дільником 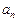 .
.
Наслідок 2. Якщо алгебраїчне рівняння з цілими коефіцієнтами
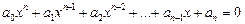
має раціональний корінь 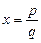 , то р — дільник
, то р — дільник 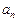 , q — дільник
, q — дільник 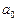 .
.
4.8. Розклад многочлена на множники
Розглянемо деякі способи розкладання многочлена на множники.
Розклад на множники
за допомогою групування
Члени многочлена групуються так, щоб вони мали спільний множник, який виноситься за дужки.
Приклад. Розв’язати рівняння
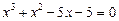 .
.
Ø Групуємо два перші та два останні члени:
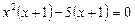 ,
,
а далі виносимо за дужки спільний множник 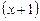 :
:
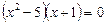 ,
, 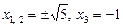 .
.
Приклад. Розглянемо рівняння
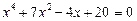 .
.
Ø Віднімемо і додамо  , а число 20 розіб’ємо на два доданки 16 і 4:
, а число 20 розіб’ємо на два доданки 16 і 4:
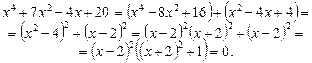
Рівняння розпадається на два рівняння:
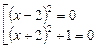
 .
.
Використання
формул скороченого множення
Приклад. Розв’язати рівняння
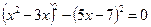 .
.
Ø Подамо ліву частину рівняння у вигляді добутку:
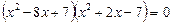 .
.
Рівняння розпадається на два рівняння:
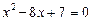 ,
, 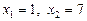
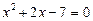 ,
, 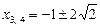 .
.
Приклад. Розв’язати рівняння
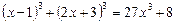 .
.
Ø Розкладемо ліву і праву частини рівняння на множники:
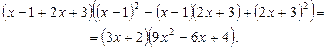
Дістанемо рівняння
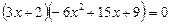 ,
,
яке розпадається на два рівняння:
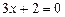 ,
, 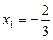 ,
,
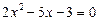 ,
, 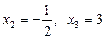 .
.
Виділення повного квадрата
або куба двочлена
Приклад. Розв’язати рівняння
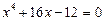 .
.
Ø Виділимо повні квадрати:
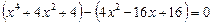 ,
,
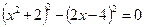 ,
, 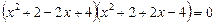 .
.
Остаточно маємо:
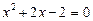 ,
, 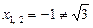 ;
;
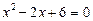 ,
, 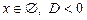 .
.
Приклад. Розв’язати рівняння
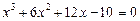 .
.
Ø Виділимо повний куб двочлена:
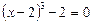 ,
, 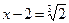 ,
, 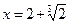 . ×
. ×
У разі виділення повного куба деякі кубічні рівняння можна перетворити до вигляду
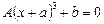 , або
, або  .
.
Далі з розкладів
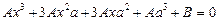 ,
,

знаходимо  за формулою:
за формулою:
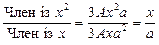 . (1)
. (1)
Приклад. Розв’язати рівняння
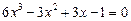 .
.
Ø Знайдемо 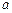 згідно з формулою (1):
згідно з формулою (1):
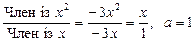 .
.
Далі, скориставшись розкладом
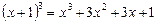 ,
,
запишемо рівняння у вигляді
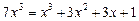 ,
, 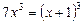 ,
,
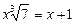 ,
, 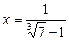 .
.
Приклад. Розв’язати рівняння
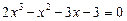 .
.
Ø Знайдемо  згідно з формулою (1):
згідно з формулою (1):
 .
.
Подавши початкове рівняння у вигляді
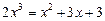 ,
,
помноживши його на 9 і скориставшись розкладом куба суми
 ,
,
дістанемо:
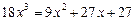 ,
, 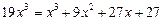 ,
,
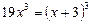 ,
, 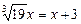
 .
.
Приклад. Розв’язати рівняння
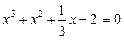 .
.
Ø Знайдемо  згідно з формулою (*):
згідно з формулою (*):
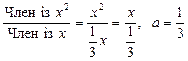 .
.
Скориставшись розкладом
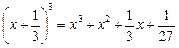 ,
,
перепишемо початкове рівняння у вигляді:
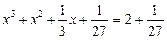 ,
, 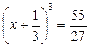 ;
;
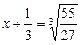 ,
, 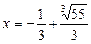 .
.
Приклад. Поділимо многочлен
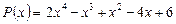
на двочлен 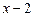 :
:

Це ділення можна виконати за схемою Горнера:
| – 1 | – 4 | ||||
| х = 2 | 2 × 2 – 1 = 3 | 2 × 3 + 1 = 7 | 2 × 7 – 4 = 10 | 2 × 10 + 6 = 26 |
Коефіцієнти частки 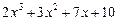 та остачу від ділення, що дорівнює 26, знаходимо за схемою Горнера.
та остачу від ділення, що дорівнює 26, знаходимо за схемою Горнера.
Приклад. Розв’язати рівняння
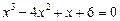 .
.
Ø Раціональні корені рівняння можуть бути лише дільниками числа 6: 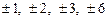 . За схемою Горнера знаходимо:
. За схемою Горнера знаходимо:
| – 4 | ||||
| х = – 1 | – 5 | |||
| х = 2 | – 3 | |||
| х = 3 |
Отже, 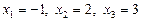 . Якщо корінь вибрано невдало, то останнє число в рядку не дорівнюватиме нулю.
. Якщо корінь вибрано невдало, то останнє число в рядку не дорівнюватиме нулю.
Приклад. Розв’язати рівняння
 .
.
Ø Раціональні корені шукаємо з-поміж дільників числа 9:  ;
; 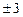 ;
; 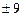 . За схемою Горнера маємо
. За схемою Горнера маємо
| – 2 | – 18 | – 6 | |||
| х = 1 | – 1 | – 19 | – 25 | – 16 | |
| х = – 1 | – 3 | – 15 | |||
| х = 3 | – 15 | – 36 | |||
| х = – 3 | – 6 |
Зі схеми випливає, що значення 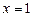 ,
, 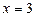 не задовольняють рівняння, а коренями будуть
не задовольняють рівняння, а коренями будуть 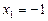 ,
,  . Часткою від ділення даного многочлена на
. Часткою від ділення даного многочлена на 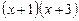 буде многочлен
буде многочлен 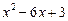 . Рівняння
. Рівняння 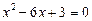 має корені
має корені 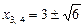 .
.
Застосування теореми Гаусса
Якщо многочлен не має раціональних коренів, то схема Горнера не прийнятна, оскільки не можна вгадати ірраціональні корені.
У такому разі потрібно спробувати розкласти многочлен з цілими коефіцієнтами на квадратні множники з цілими коефіцієнтами.
Приклад. Розв’язати рівняння
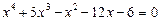 .
.
Ø Це рівняння не має раціональних коренів.
Спробуємо розкласти даний многочлен на два квадратні множники з цілими коефіцієнтами:
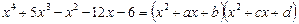 .
.
Розкриваючи дужки і зрівнюючи коефіцієнти при однакових степенях 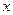 , дістаємо систему рівнянь:
, дістаємо систему рівнянь:
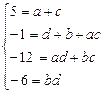 ,
,
де 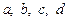 — цілі числа. З останнього рівняння знаходимо, що можливі такі випадки:
— цілі числа. З останнього рівняння знаходимо, що можливі такі випадки:
1) 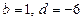 ; 2)
; 2) 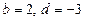 ; 3)
; 3) 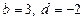 ; 4)
; 4) 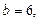
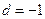 ; 5)
; 5) 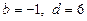 ; 6)
; 6) 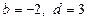 ; 7)
; 7) 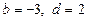 ; 8)
; 8) 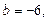
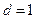 .
.
Оскільки квадратичні множники перестановочні, то випадки 1—4 повторюють випадки 5—8. Тому розглядатимемо лише випадки 1—4.
1. 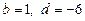 . Із системи рівнянь
. Із системи рівнянь
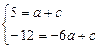
знаходимо 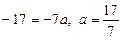 .
.
Оскільки  не є цілим числом, то розкладання на квадратичні множники з цілими коефіцієнтами неможливе.
не є цілим числом, то розкладання на квадратичні множники з цілими коефіцієнтами неможливе.
2. 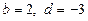 . З системи рівнянь
. З системи рівнянь
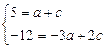
знаходимо 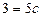 .
.
Значення 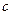 не є цілим числом.
не є цілим числом.
3. 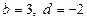 . Із системи рівнянь
. Із системи рівнянь
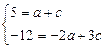
знаходимо 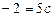 .
.
Значення 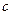 не є цілим числом.
не є цілим числом.
4. 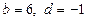 . Із системи рівнянь
. Із системи рівнянь
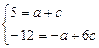
знаходимо 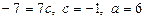 .
.
Перевіряємо, чи виконується рівність  :
: 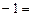
 . Отже, маємо розклад на множники:
. Отже, маємо розклад на множники:
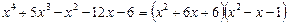 .
.
Розв’язуємо відповідні квадратні рівняння:
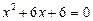 ,
, 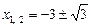 ,
,
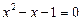 ,
, 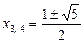 . ×
. ×
Корені щойно розглянутого рівняння — ірраціональні числа. Проте викладений спосіб розкладання на множники можна застосовувати й у разі, коли рівняння має раціональні корені.
Приклад. Розв’язати рівняння
 .
.
Ø Шукаємо розклад лівої частини рівняння на квадратні множники у вигляді:
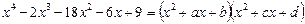 .
.
Приходимо до системи рівнянь із цілими коефіцієнтами 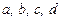 :
:
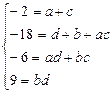 .
.
Узявши 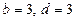 , дістанемо систему рівнянь
, дістанемо систему рівнянь
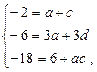
звідки знайдемо 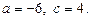
Отже, маємо шуканий розклад на множники:
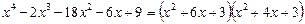 .
.
Остаточно маємо:
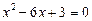 ,
, 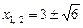 ,
,
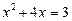 ,
,  .
.
4.9. Рівняння, що зводяться до квадратних рівнянь
Розглянемо типи рівнянь, які зводяться до квадратних.
Двочленні рівняння
Двочленними рівняннями називають рівняння виду
 ,
, 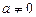 .
.
Розв’язок рівнянь складається в розкладанні рівняння на множники.
Приклад. Розв’язати рівняння
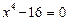 .
.
Ø Розкладаючи ліву частину рівняння на множники, дістаємо:
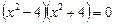 ,
, 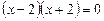 ,
,  .
.
Тричленні рівняння
Тричленними рівняннями називають рівняння виду
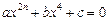 ,
, 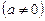 .
.
Заміною  зводимо тричленне рівняння до квадратного.
зводимо тричленне рівняння до квадратного.
Приклад. Розв’язати рівняння 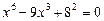 .
.
Ø Виконавши заміну 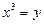 , дістанемо
, дістанемо 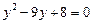 , звідки
, звідки 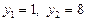 ,
, 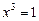 ,
, 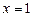 ,
, 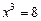 ,
,  .
.
При 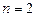 тричленне рівняння називають біквадратним.
тричленне рівняння називають біквадратним.
Приклад. Розв’язати рівняння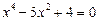 .
.
Ø 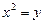 ,
, 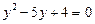 ,
, 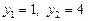 ,
, 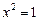 ,
,  ,
, 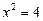 ,
, 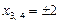 .
.
Заміна змінної в рівнянні
Приклад. Розв’язати рівняння
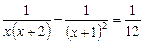 .
.
Ø Виконавши заміну 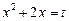 , дістанемо
, дістанемо
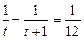 ,
,
звідки випливає квадратне рівняння  ,
, 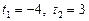 .
.
Повертаючись до попередніх позначень дістаємо:
якщо 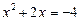 , то
, то 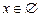 ; якщо
; якщо 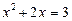 ,
, 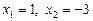 .
.
Попереднє перетворення рівнянь
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1295; Нарушение авторских прав?; Мы поможем в написании вашей работы!