Метод условной линеаризации

1. Рассмотрим включение постоянной э.д.с. Е в цепь, состоящую из последовательно соединенных катушки ин­дуктивности L и нелинейного резистора, характеристика которого u=f(i) задана графически (рис. 13.1, а).

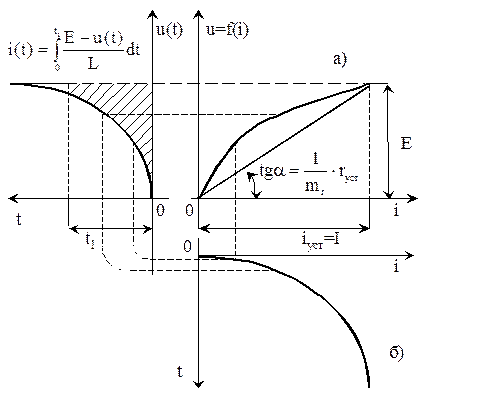
Рис. 13.1. Метод условной линеаризации (цепь с нелинейным резистором)

Дифференциальное уравнение

(13.1)

является нелинейным. Условимся сначала считать, что характеристика резистора линейна и проходит через точку с координатами I и Е, соответствующими установившемуся режиму. Тогда r=E/I=const и дифференциальное урав­нение (13.1)

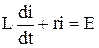
имеет решение

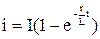. (13.2)

По этой зависимости i (t), изображенной на рис. 13.2, и нелинейной характеристике рис. 13.1, а строится кривая u(t) на рис. 13.1, в.

На основании (13.1)

.

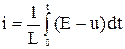Следовательно, для произвольного момента t₁ соответ­ствующий ток определится выражением

,

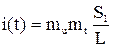где m_u — масштаб напряжения, В/мм;

m_t — масштаб времени, с/мм;

S₁ — заштрихованная на рис. 13.1, в площадь, мм².

Задаваясь различными t, можно построить кривую, более точно выражающую зависимость тока от времени, чем приближенное решение (13.2).

Полученная кривая тока может быть использована для последующего уточнения решения, если в этом окажется необходимость.

2. Если цепь состоит из резистора и нелинейной ка­тушки индуктивности, то в случае включения постоянной э.д.с. дифференциальное уравнение имеет вид:

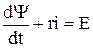(13.3)

Нелинейная характеристика условно заменяется линей­ной, проходящей через точку с координатами Y_уст и I, соответствующими установившемуся режиму. Тогда L=Y_уст/I = const и дифференциальное уравнение

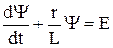
имеет решение

.

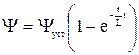По кривой Y(t) и заданной нелинейной характери­стике Y(i) строится кривая i(t), дающая приближенное решение (рис. 13.2).

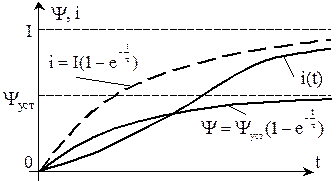
Рис. 13.2. Метод условной линеаризации (цепь с нелинейной индуктивностью)

Для сравнения на рис. 13.2 пунктиром изображена функция 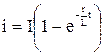, получающаяся при условии, что L=const. Так как при малых токах дифференциальная индуктивность больше, чем L, а при боль­ших токах — меньше L, то вначале ток нарастает медлен­нее, чем при постоянной индуктивности L, а затем — быст­рее.

Дата добавления: 2014-01-15