Метод кусочно-линейной аппроксимации

Сущность метода пояснена ниже на примере включе­ния источника постоянной э.д.с. в цепь с нелинейным со­противлением и линейной индуктивностью, соединенными последовательно. Характеристика нелинейного сопротив­ления u=f(i) задана графически и показана на рис. 13.3 пунктиром.

Дифференциальное уравнение имеет вид (13.1).

Заменим нелинейную характеристику некоторой лома­ной линией (рис. 13.3):

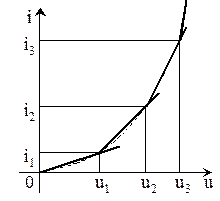
Рис. 13.3. Замена нелинейной характеристики ломаной линией

Для первого участка:

,

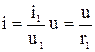откуда u=r₁i, где r₁=u₁/i₁;

для второго участка:

,

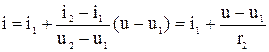откуда

,

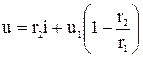где

;

для третьего участка:

,

откуда

,

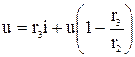где

.

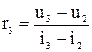Подставляя указанные значения в дифференциальное уравнение

,

получаем:

для первого участка

для второго участка:

для третьего участка:

Решения дифференциальных уравнений для участков имеют вид:

при 0<t<t₁;

при t₁<t<t₂;

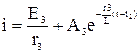при t₂<t<t₃.

Постоянная интегрирования А₁ находится из условия, что i=0 при t=0, откуда А₁=-E₁/r₁.

Для первого участка

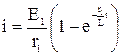при 0<t<t₁.

Подстановка в полученное уравнение t = t₁ и i=i₁ дает:

,

откуда определяется момент времени t₁.

Постоянная A₂ определяется из уравнения тока для второго участка: i=i₁ при t=t₁ откуда А₂=i₁-E₂/r₂.

Уравнение тока для второго участка

при t₁<t<t₂.

Момент времени t₂ находится из условия, что i=i₂ при t=t₂

.

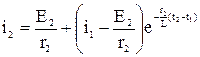Полученное уравнение легко решается относительно t₂.

Ясен также порядок определения А₃ и последующих постоянных интегрирования в случае большого числа уча­стков.

По уравнениям для токов различных участков может быть построена кривая i=f(t), характер которой показан на рис. 13.4.

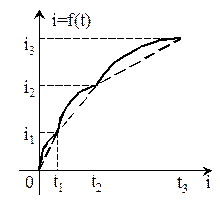
Рис. 13.4. Метод кусочно-линейной аппроксимации

Рассмотренный метод расчета основан на методе припасовывания, суть которого состоит в том, что начальное значение тока в некотором n-м участке приравнивается конечному значению тока в предыдущем n-1-м участке, а конечное значение тока в n-м участке приравнивается начальному значению тока в последующем n+1-м участке.

Необходимость такого приравнивания вытекает из того положения, что ток в местах стыка рассматриваемых участ­ков не может изменяться скачком. Поскольку истинная кривая тока в рассматриваемом случае не может также иметь разрывов производной, на рис. 13.4 изображена пунктирная кривая, представляющая более правильно ис­тинный ток.

Пример. Линейный резистор r=7,5 Ом, катушка индуктив­ности L=6,5 Гн, соединенные последовательно, подключаются к источ­нику постоянной э.д.с. Е=12,1 В через диод, характеристика кото­рого задана графически (рис. 13.5).

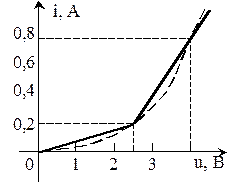
Рис. 13.5. Пример

Требуется найти переходный ток.

Характеристика диода заменяется двумя отрезками прямых. Конец первого участка соответствует i₁= 0,2 А, u₁=2,5 В; конец второго участка соответствует i₂=0,8 A, u₂=4 В. Сопротивления и э.д.с.:

Ом, Е₁=12,1 В;

Ом;

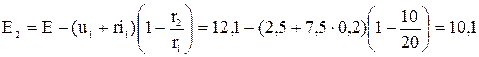В.

Дифференциальное уравнение для первого, участка:

.

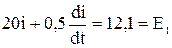Дифференциальное уравнение для второго участка:

.

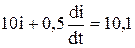Ток для первого участка:

.

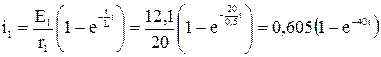Из выражения

получается t₁=0,01 c.

Ток для второго участка:

.

Дата добавления: 2014-01-15