Властивості і характеристики потоків викликів

Випадкові потоки викликів класифікуються в залежності від наявності або відсутності трьох наступних властивостей: стаціонарності, післядії і ординарності.

Стаціонарність означає, що з плином часу імовірнісні характеристики потоку не змінюються. Інакше кажучи, для стаціонарного потоку ймовірність надходження i викликів за проміжок довжиною t залежить тільки від величини проміжку і не залежить від його розташування на осі часу. Реально поступаючий, наприклад на ГТС або МТС, потік викликів має явно виражений нестаціонарний характер. Проте усередині діб завжди можна виділити одно-або двогодинні проміжки, протягом яких поступаючий потік викликів близький до стаціонарного.

Післядія означає залежність імовірнісних характеристик потоку від попередніх подій. Іншими словами, ймовірність надходження викликів в проміжок [ t ₁, t ₂) залежить від числа, часу надходження і тривалості обслуговування викликів до моменту t ₁. Потік викликів, що надходять від досить великої групи джерел, близький за своїми властивостями до потоку без післядії, якщо при цьому не враховувати повторних викликів. Потік від малої групи, навпаки, має помітну післядією.

Ординарність означає практичну неможливість групового надходження викликів. Інакше кажучи, можливість надходження двох або більше викликів за будь-який нескінченно малий проміжок часу D t є величина нескінченно мала більш високого порядку ніж Dt. тобто Р_i ³ 2 (Dt) =0(D t).

У мережах зв'язку потоки викликів, як правило, ординарні. При обробці телеграм оператором можлива неординарність потоку, якщо передбачається надходження телеграм партіями. В інших областях техніки неординарні потоки зустрічаються частіше. Наприклад, при розрахунку систем ППО необхідно враховувати, що виклики - літаки супротивника - можуть надходити по одному і групами.

До основних характеристик випадкового потоку відносять провідну функцію, параметр і інтенсивність. Провідна функція випадкового потоку (0,1) є математичне сподівання числа викликів в проміжку [0, t). Функція (0,1) невід'ємна, неспадаюча і в практичних задачах теорії телетрафіка неперервна і приймає тільки кінцеві значення.

Параметр потоку l(t) в момент часу t є межа відношення ймовірності надходження не.менше одного виклику в проміжку [ t, t +D t) до величини цього проміжку D t при D t ®0. Параметр потоку визначає щільність ймовірності настання викликаючого моменту в момент t. Визначення параметра рівносильно припущенням, що ймовірність надходження хоча б одного виклику в проміжку [ t, t + Δ t) з точністю до нескінченно малої о(Δt) пропорційна проміжку Δt і параметру потоку l(t): Pi³2(t,t+Δt)= l(t) Δt+o(Δt). Для стаціонарних потоків ймовірність надходження викликів не залежить від часу, Pi³2(t,t+Δt)= Pi³2(Δt), тому параметр стаціонарного потоку постійний. 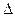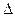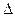Відповідно отримуємо P_{i³ 1}( t) = l (t) t+o (t).

Інтенсивність стаціонарного потоку m є математичне сподівання числа викликів в одиницю часу. Для нестаціонарних потоків використовуються поняття середньої та миттєвої інтенсивності. Середня інтенсивність потоку в проміжку [ t ₁, t ₂) є математичне сподівання числа викликів у цьому проміжку в одиницю часу. Середню інтенсивність потоку можна виразити через провідну функцію: m(t ₁, t ₂)= [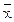(o, t ₂)-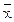(o, t ₁)]/(t ₂, t ₁). Миттєва інтенсивність потоку m(t) в момент t є похідна провідної функції потоку по t.
Якщо миттєва інтенсивність характеризує потік викликів, то параметр - потік викликаючих моментів. Тому завжди m(t)≥ l (t), а рівність має місце тільки для ординарних потоків, коли в кожен викликаючий момент надходить тільки один виклик.

При розгляді конкретних математичних моделей потоків їх розподіляють на три класи: потоки без післядії, з простою і обмеженою післядією. В клас потоків без післядії входять: найпростіший, Пуассонівський зі змінним або випадковим параметром, неординарний Пуассонівський і Пуассонівський з неординарними викликами. До потоків з простою післядією відносяться: примітивний, згладжений і з повторними викликами. Обмеженою післядією володіють рекурентний потік, потік Пальма, потік Ерланга.

Дата добавления: 2014-01-11