Примітивний потік

Ординарный поток, параметр которого 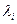пропорционален числу свободных источников N_i - в состоянии обслуживающей системы i, называется примитивным:

(1.17

Здесь a-параметр (интенсивность) источника в свободном состоянии; N -общее число источников; i -число занятых источников.

Примитивный поток в литературе иногда называют пуассоновским потоком второго рода или потоком чистой случайности второго рода, а также энгсетовским потоком. Первые два названия связаны с тем, что наряду с простейшим (поток первого рода) при- митивный поток используется для описания процесса поступлении вызовов от первичных источников. Модель примитивного потока учитывает так называемый эффект конечного числа источников: новые вызовы могут поступать только от свободных источников. Это определяет скачкообразное изменение параметра потока, причём наибольшее значение параметр принимает, когда все источники свободны, и наименьшее, когда число занятых источнике достигает максимума. Это свойство примитивного потока существенным образом влияет на процесс обслуживания и заметно повышает пропускную способность обслуживающей системы.

Распределение промежутка свободности подчиняется показательному закону с параметром a:•'

. (1.19)

Это равносильно предположению, что новые вызовы от источника поступают случайно независимо от моментов возникновени и окончания обслуживания предыдущих вызовов.

Примитивный поток является более общим понятием по сравнению с простейшим. С ростом числа источников N и соответствующим уменьшением a последействие примитивного потока сокращается. В пределе при ограниченном значении i и N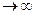, а , но так, что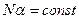, примитивный поток переходит в простейший с параметром l= Na. Практически уже при N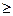З00—500 (в зависимости от величины a и максимального значения i) можно пользоваться более простой моделью простейшего потока. Вносимая при этом погрешность невелика.

Дата добавления: 2014-01-11