
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрическое поле линейного заряда
|
|
|
|
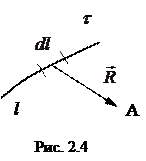 Пусть проводник, длиной l, несет заряд q с линейной плотностью
Пусть проводник, длиной l, несет заряд q с линейной плотностью 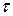 , значение которой в каждой точке задано (см. рис. 2.4).
, значение которой в каждой точке задано (см. рис. 2.4).
Выделим на проводнике бесконечно малый отрезок  . Элементарный заряд
. Элементарный заряд 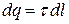 можно рассматривать как точечный, а значит, согласно (2.4), напряжённость поля в точке наблюдения
можно рассматривать как точечный, а значит, согласно (2.4), напряжённость поля в точке наблюдения
 , (2.10)
, (2.10)
где R – расстояние от элементарного заряда 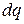 до точки наблюдения. Напряжённость поля, созданная всем заряженным проводником,
до точки наблюдения. Напряжённость поля, созданная всем заряженным проводником,
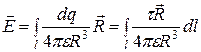 . (2.11)
. (2.11)
Интегрирование ведется по всей длине проводника, где 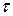 отлична от нуля.
отлична от нуля.
Если электрическое поле создается линейным, поверхностным, объемным и точечным зарядами, то для определения напряженности поля, созданного этой системой зарядов, применяется принцип наложения (суперпозиции)
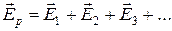 .
.
2.8. Линии вектора напряжённости („силовые" линии).
Из изложенного выше следует, что в любой точке электрического поля, образованного произвольным распределением зарядов, может быть определён вектор напряжённости электрического поля  .
.
Для графического изображения и наглядного представления электрического поля введено понятие линии вектора напряжённости („силовой" линии).
Силовая линия — это мысленно проведенная в поле линия, начинающаяся на положительно заряженном теле и заканчивающаяся на отрицательно заряженном теле. Проводится она таким образом, что касательная к ней в любой ее точке дает направление напряженности поля  в этой точке. силовые линии имеют начало (на положительно заряженном теле) и конец (на отрицательно заряженном теле). Так как положительный и отрицательный заряды, создающие поле, не могут быть в одной и той же точке, то силовые линии электростатического поля не могут быть линиями, замкнутыми сами на себя.
в этой точке. силовые линии имеют начало (на положительно заряженном теле) и конец (на отрицательно заряженном теле). Так как положительный и отрицательный заряды, создающие поле, не могут быть в одной и той же точке, то силовые линии электростатического поля не могут быть линиями, замкнутыми сами на себя.
 Так как в каждой точке поля вектор
Так как в каждой точке поля вектор  имеет вполне определенное направление (за исключением точек, где
имеет вполне определенное направление (за исключением точек, где  равно нулю), то через каждую точку поля можно провести только одну линию вектора
равно нулю), то через каждую точку поля можно провести только одну линию вектора  .
.
Дифференциальное уравнение „силовых" линий:
 (2.12)
(2.12)
Решение дифференциального уравнения (2.12) представляет собой уравнение линии вектора  .
.
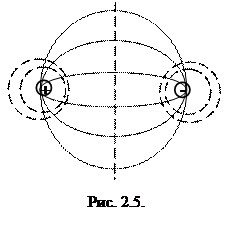
На рис. 2.5 с помощью силовых линий (сплошные линии) показано поле разноименных зарядов.
2.9. Поток вектора  .
.
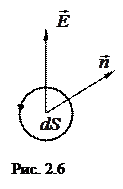 В электрическом поле выделим бесконечно малый элемент площадки
В электрическом поле выделим бесконечно малый элемент площадки 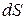 и восстановим в какую-либо сторону единичный, нормальный к этому элементу, вектор
и восстановим в какую-либо сторону единичный, нормальный к этому элементу, вектор 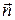 (рис. 2.6). Элементарный поток вектора
(рис. 2.6). Элементарный поток вектора  сквозь площадку dS есть величина скалярная, равная
сквозь площадку dS есть величина скалярная, равная
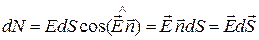 ,
,
где  - вектор, длина которого численно равна площади элемента поверхности dS, а направление совпадает с направлением единичного вектора
- вектор, длина которого численно равна площади элемента поверхности dS, а направление совпадает с направлением единичного вектора 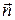 .
.
В зависимости от угла между  и
и 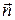 поток вектора
поток вектора  может иметь тот или иной знак (если угол острый, то знак потока положительный, если тупой — отрицательный). Обычно направление единичного вектора
может иметь тот или иной знак (если угол острый, то знак потока положительный, если тупой — отрицательный). Обычно направление единичного вектора 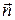 связывают с обходом элемента площадки dS по правовинтовой системе.
связывают с обходом элемента площадки dS по правовинтовой системе.
Поток вектора  сквозь поверхность S равен
сквозь поверхность S равен
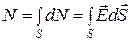 . (2.13)
. (2.13)
При  говорят про исток вектора
говорят про исток вектора  , а при
, а при 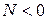 - про сток вектора.
- про сток вектора.
Если поверхность замкнута, то поток вектора  сквозь замкнутую поверхность определится
сквозь замкнутую поверхность определится
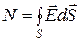 . (2.14)
. (2.14)
При этом условно будем считать положительной внешнюю нормаль к замкнутой поверхности.
Если поверхность, сквозь которую определяют поток вектора, замкнутая, то на знаке интеграла ставят кружок.
В теории поля проявляют интерес не только к наличию потоку вектора, а и к тому, в какой точке находится источник вектора. Для определения источника поля в каждой точке пространства вводят понятие дивергенции вектора.
2.10. Дивергенция вектора  .
.
Для описания векторного поля введена скалярная величина, которая называется дивергенцией или расходимостью вектора. Нахождение дивергенции является операцией дифференцирования векторной величины по координатным направлениям.
 Пусть некоторый объем V находится в поле вектора
Пусть некоторый объем V находится в поле вектора  . Разобьем поверхность, которая ограничивает объем, на бесконечно малые элементы dS (рис. 2.7).
. Разобьем поверхность, которая ограничивает объем, на бесконечно малые элементы dS (рис. 2.7).
Будем считать внешнюю нормаль, проведенную к поверхности объема, положительной. Тогда вектор 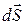 будет направлен наружу. Поток вектора
будет направлен наружу. Поток вектора  сквозь поверхность, которая ограничивает объем, равен
сквозь поверхность, которая ограничивает объем, равен
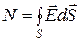 .
.
Предел, к которому стремится отношение полного потока вектора через замкнутую поверхность к величине ограничиваемого ею объема при бесконечном уменьшении последнего, называется дивергенцией или расходимостью вектора.
Дивергенция — скалярная величина; она положительна, если линии поля начинаются в бесконечно малом объеме, и отрицательна, если линии поля заканчиваются в этом объеме.
Поля, в которых полный поток вектора через любую замкнутую поверхность равен нулю, называются бездивергентными.
Определение дивергенции вектора  можно выразить математически
можно выразить математически
 . (2.15)
. (2.15)
Дивергенция вектора  в прямоугольных координатах
в прямоугольных координатах
 , (2.16)
, (2.16)
где 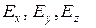 - составляющие вектора по координатным осям.
- составляющие вектора по координатным осям.
Дивергенция вектора  в точке, в которой отсутствует заряд, равна нулю.
в точке, в которой отсутствует заряд, равна нулю.
Дивергенция вектора  во всех точках пространства электрического поля равна нулю, если в данном пространстве отсутствуют заряды.
во всех точках пространства электрического поля равна нулю, если в данном пространстве отсутствуют заряды.
Если электрическое поле создано положительным зарядом, то внутри области, в которой находится заряд, будет исток поля вектора  , если отрицательным, то - сток. Если внутри области нет зарядов, то нет ни истоков, ни стоков поля, а значит,
, если отрицательным, то - сток. Если внутри области нет зарядов, то нет ни истоков, ни стоков поля, а значит, 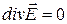 (рис. 2.8). Следовательно, дивергенция характеризует векторное поле в каждой его точке с точки зрения наличия истоков или стоков поля.
(рис. 2.8). Следовательно, дивергенция характеризует векторное поле в каждой его точке с точки зрения наличия истоков или стоков поля.
 |
2.11. Дифференциальный оператор «набла».
Вычисление дивергенции представляет собой операцию сложного дифференцирования векторной величины покоординатам. Для обозначения этой операции вводят символ 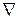 (набла)
(набла)
 (2.17)
(2.17)
где 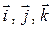 — единичные векторы по соответствующим координатам.
— единичные векторы по соответствующим координатам.
Выражение дивергенции можно рассматривать, как скалярное произведение вектора 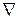 и вектора
и вектора
 .
.
Следовательно, в прямоугольной системе координат
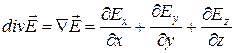 . (2.18)
. (2.18)
Применение оператора 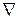 к скалярной функции дает другой дифференциальный оператор – градиент
к скалярной функции дает другой дифференциальный оператор – градиент
 .
.
Физически градиент определяет скорость изменения функции в направлении ее максимального роста.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1535; Нарушение авторских прав?; Мы поможем в написании вашей работы!