Работа сил электрического поля. потенциал

Теорема Гаусса в дифференциальной форме позволяет решить обратную задачу электростатики (по заданному закону изменения вектора напряженности найти закон изменения заряда, возбуждающего поле). Для решения прямой задачи этого уравнения недостаточно (прямая задача – определение поля по заданному заряду). Для облегчения анализа и расчета полей вводят расчетную скалярную 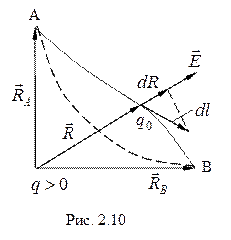функцию 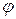- потенциал.

Пусть поле возмущается зарядом 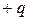. Найдем работу поля при перемещении пробного заряда 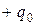из точки А в точку В (см. рис. 2.10). Если заряд переместился на расстояние dl, то работа сил поля

,

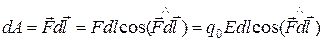где формально рассматривается как вектор, направленный по касательной, а длина его равна отрезку пути dl.

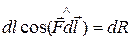, тогда

работа сил по перемещению заряда 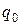на пути l равна

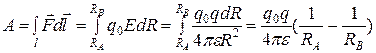. (2.22)

Работа по перемещению заряда в электрическом поле не зависит от вида пути, а зависит от начального и конечного положения заряда.

Поле, работа сил которого не зависит от вида пути, называется потенциальным полем.

Из (2.22) следует, что работа по замкнутому пути равна нулю, т.е.

.

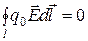Если пробный заряд 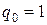, то работа по замкнутому контуру

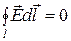. (2.23)

Этот интеграл называют циркуляцией вектора (поле потенциально).

Если пробный заряд 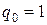, то работа определится

.

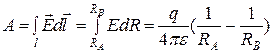Если пробный заряд 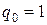переместился в бесконечно удаленную точку (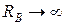), тогда

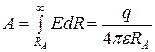
Потенциал – это энергетическая характеристика каждой точки поля; численно потенциал равен работе сил поля, совершаемой при перемещении единицы заряда из данной точки поля в бесконечность (потенциал бесконечности принят равным нулю).

.

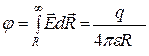Единица измерения потенциала – В (вольт).

Если поле создается несколькими зарядами, то потенциал в любой точке равен сумме потенциалов составляющих полей

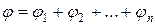
Если поле создается объемным зарядом, то, разбивая объем на бесконечно малые объемы и считая заряд этих объемов точечным (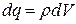), по принципу наложения результирующий потенциал

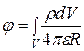, (2.24)

где R – расстояние от точки наблюдения до бесконечно малого объема dv.

Аналогично для системы поверхностно распределенных зарядов

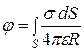, (2.25)

и для системы линейно распределенных зарядов

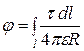. (2.26)

Пусть пробный заряд q ₀ = 1 перемещается в электрическом поле, созданном точечным зарядом, от точки А к точке В. При этом работа сил электрического поля определиться как

, (2.27)

т.е. работа, совершаемая электрическим полем при перенесении единицы заряда, численно равна разности потенциалов между точками А и В.

Разность потенциалов называется электрическим напряжением и обозначается буквой U.

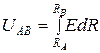(2.28)

В электрическом поле, созданном произвольно распределенными зарядами, можно провести поверхности, в различных точках которых потенциал является величиной постоянной. Эти поверхности называются эквипотенциальными поверхностями (эквипотенциали). Они описываются уравнением

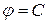, где С – постоянная величина.

На эквипотенциалях разность потенциалов между любыми двумя точками равна нулю, т.е.

.

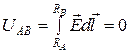Это условие выполняется в том случае, если , следовательно, эквипотенциали должны быть нормальны к силовым линиям. Эквипотенциальные поверхности показаны пунктирными линиями на рис. 2.5.

При движении заряда вдоль эквипотенциальной поверхности работа поля не совершается.

При переходе из одной точки электрического поля в другую потенциал в общем случае меняется. Скорость изменения потенциала в направлении быстрейшего его роста, т.е. в направлении, нормальном к эквипотенциалям, называется градиентом потенциала

, (2.29)

где 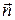- единичный вектор, направленный по нормали к эквипотенциальной поверхности.

В декартовой системе координат

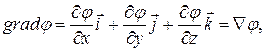(2.30)

где 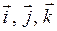— единичные векторы по соответствующим координатам.

Дата добавления: 2014-01-15