Интегрирование тригонометрических функций

Вопрос

Вопрос

Вопрос

Интегрирование рациональных функций

Для интегрирования рациональной функции 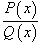, где P (x) и Q (x) - полиномы, используется следующая последовательность шагов:

1. Если дробь неправильная (т.е. степень P (x) больше степени Q (x)), преобразовать ее в правильную, выделив целое выражение;

 

1. Разложить знаменатель Q (x) на произведение одночленов и/или несократимых квадратичных выражений;

 

1. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

 

1. Вычислить интегралы от простейших дробей.

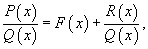Рассмотрим указанные шаги более подробно. Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P (x) больше степени знаменателя Q (x)), разделим многочлен P (x) на Q (x). Получим следующее выражение: где 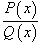- правильная рациональная дробь. Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q (x) в виде 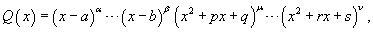где квадратичные функции являются несократимыми, то есть не имеющими действительных корней. Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде: 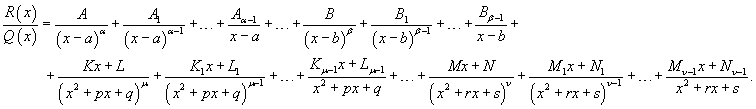Общее число неопределенных коэффициентов A_i, B_i, K_i, L_i, M_i, N_i,... должно быть равно степени знаменателя Q (x). Затем умножим обе части полученного уравнения на знаменатель Q (x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов A_i, B_i, K_i, L_i, M_i, N_i,.... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов. Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: 1.   2. 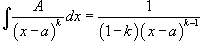У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: 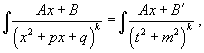где 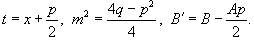Затем применяются следующие формулы: 3. 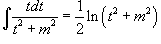  4.   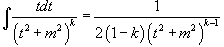5. 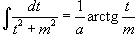Интеграл 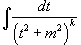может быть вычислен за k шагов с помощью формулы редукции 6.

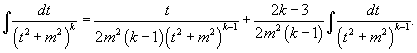
Пример 1

Вычислить интеграл 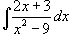. Решение. Разложим подынтегральное выражение на простейшие дроби: 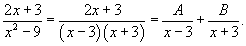Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями: 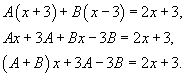Следовательно, 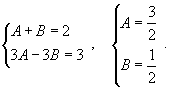Тогда 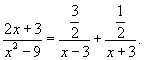Теперь легко вычислить исходный интеграл

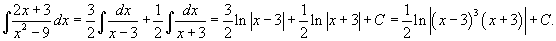
Пример 2

Вычислить интеграл 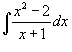. Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. 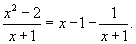Получаем

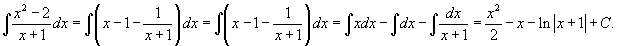
Пример 3

Вычислить интеграл 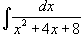. Решение.

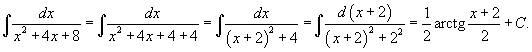
Пример 4

Вычислить интеграл 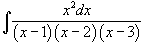. Решение. Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов: 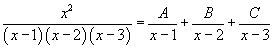Определим ы: 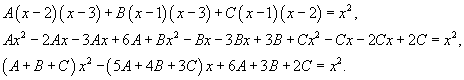Следовательно, 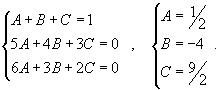Получаем 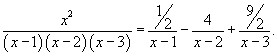Интеграл, соответственно, равен

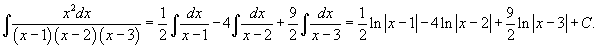
Пример 5

Найти интеграл 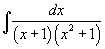. Решение. Разложим подынтегральное выражение на сумму двух дробей. 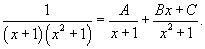Найдем неизвестные коэффициенты. 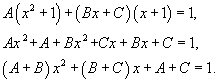Отсюда получаем 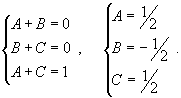Подынтегральное выражение представляется в виде 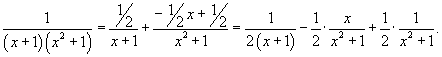Исходный интеграл равен

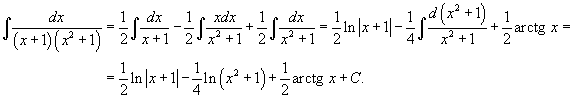
Пример 6

Найти интеграл 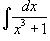. Решение. Разложим знаменатель в подынтегральном выражении на множители: 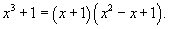Далее представим подынтегральное выражение в виде суммы простейших дробей 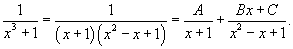Определим коэффициенты: 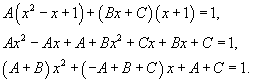Следовательно, 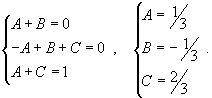Отсюда находим 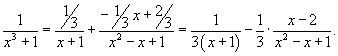Теперь вычислим исходный интеграл

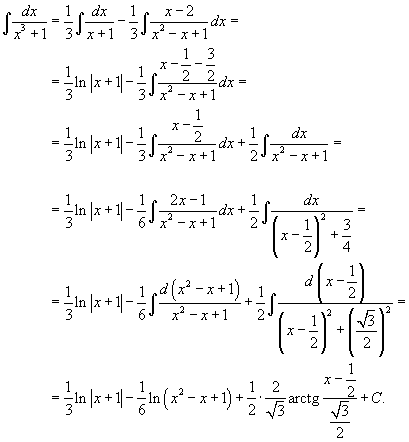
Пример 7

Вычислить интеграл 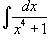. Решение. Перепишем знаменатель рациональной дроби в следующем виде: 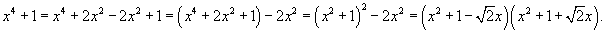Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде 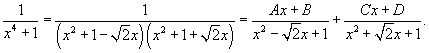Определим неизвестные коэффициенты. 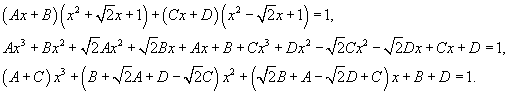Получаем 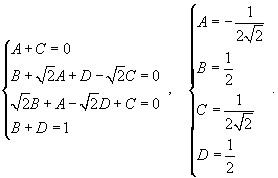Следовательно, 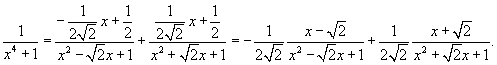Интегрируем каждое слагаемое и находим ответ.

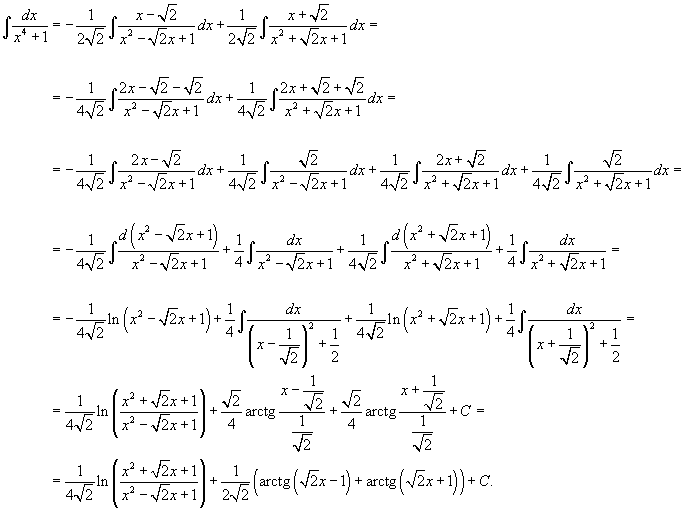
Пример 8

Вычислить интеграл 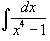. Решение. Разложим знаменатель на множители: 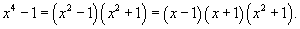Запишем подынтегральную дробь в виде суммы простейших дробей. 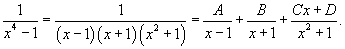Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений. 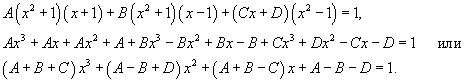Следовательно, 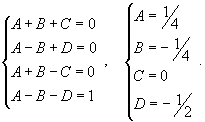Таким образом, подынтегральное выражение представляется в виде 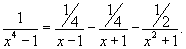Окончательно находим

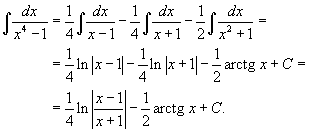
Пример 9

Вычислить интеграл 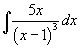. Решение. Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка: 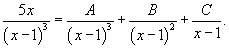Определим неизвестные коэффициенты. 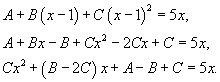Получаем систему уравнений 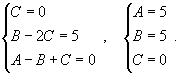Следовательно, 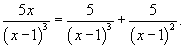Исходный интеграл равен

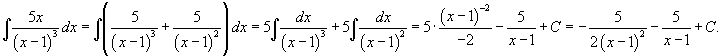
Пример 10

Вычислить интеграл 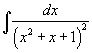. Решение. Поскольку 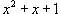- несократимый квадратный трехчлен, выделим в знаменателе полный квадрат: 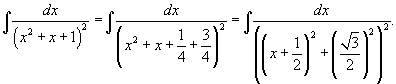Найдем полученный интеграл с помощью формулы редукции 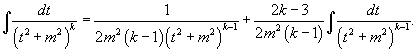Получаем ответ:

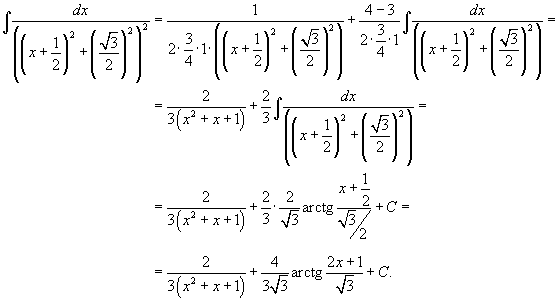
Интегрирование некоторых иррациональных функций

1. Интегралы вида 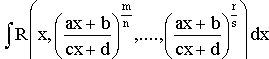рационализируются подстановкой 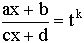, где 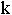- общий знаменатель дробей .
2. Интеграл от дифференциального бинома 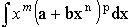выражается через конечную комбинацию элементарных функций лишь в трех случаях:
2.1. - целое число, подстановка 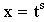( 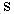- наименьший общий знаменатель дробей ).
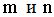2.2. 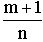- целое число, подстановка 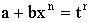( 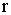- знаменатель дроби ).
2.3. 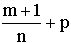- целое число, подстановка 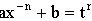( 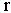- знаменатель дроби ).

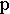В остальных случаях интеграл от дифференциального бинома не выражается через конечное число элементарных функций.

3. Интеграл вида 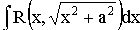, подстановка .
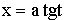4. Интеграл вида 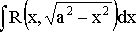, подстановка 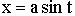или .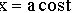
5. Интеграл вида 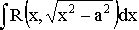, подстановка 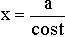или .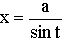
6. Интеграл вида 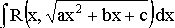с помощью подстановки 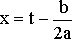сводится к одному из интегралов (3) – (5).
7. Интеграл вида 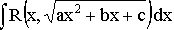можно также упростить подстановками Эйлера:
7.1. Если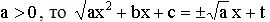
7.2. Если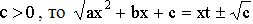
7.3. Если трехчлен 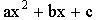имеет различные корни 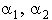, то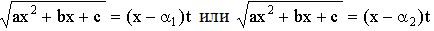

Интегрирование дифференциальных биномов

Выражение вида,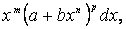 где m, n, p, a, b - постоянные числа, называемые дифференциальным биномом.

Интеграл 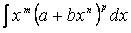может быть выражен через элементарные функции в следующих случаях:

1) p - есть целое число,

2) 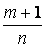- целое число,

3) 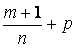- целое число,

Доказательство:

преобразуем данный интеграл с помощью подстановки

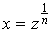, dx =, (2-138)

тогда

=

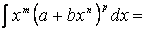
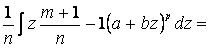
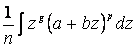где .

Пусть p целое число. Тогда g - есть рациональное число и его можно обозначить через 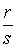. И тогда интеграл примет вид . Этот интеграл берется подстановкой .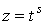

. Пусть 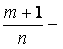целое число. Тогда тоже целое число и интеграл решается подстановкой 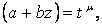где u есть знаменатель рационального числа ,.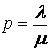

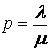. Пусть 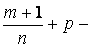целое число, тогда 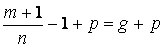тоже есть целое число.

Тогда 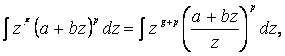его берут с помощью подстановки 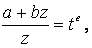где e -есть знаменатель числа .

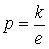Пример 1.

Дан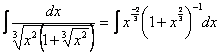

Здесь p = -1 (целое число). Положим 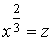. Тогда ,.

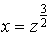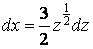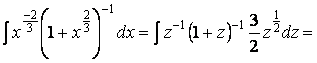
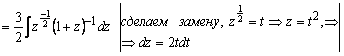
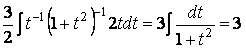=arctg t +c=3arctga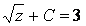rctg.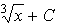

Пример 2.

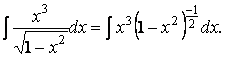Здесь m=3; n=2; 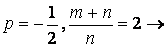целое число.

Делаем замену 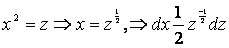, тогда

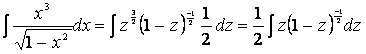. Сделаем подстановку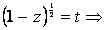 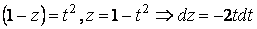, следовательно,

.

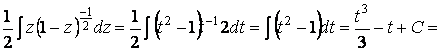
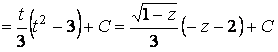Пример 3.

.

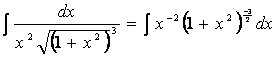Здесь m=-2, n=2,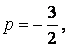 причем 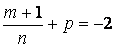(целое число).

Сведем выражение в скобках к линейной функции

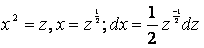
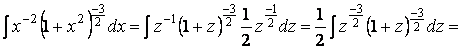
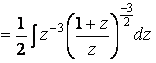, сделаем замену 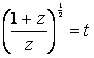тогда 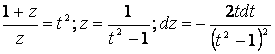, следовательно,

=

-.

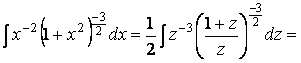
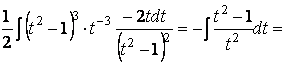
Доказательство, того, что биномиальное выражение может быть проинтегрировано только в этих трех случаях, можно выразить через элементарные функции, выполнил знаменитый русский математик П. Л. Чебышев.

Множество задач сводится к нахождению интегралов трансцендентных функций, содержащих тригонометрические функции. В данной статье сгруппируем наиболее часто встречающиеся виды подынтегральных функций и на примерах рассмотрим методы их интегрирования.

· Начнем с интегрирования синуса, косинуса, тангенса и котангенса.

Из таблицы первообразных сразу заметим, что 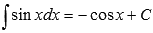и .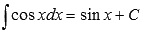

Метод подведения под знак дифференциала позволяет вычислить неопределенные интегралы функций тангенса и котангенса:

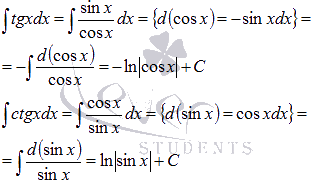
К началу страницы

· Поясним, как были найдены формулы 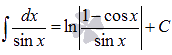и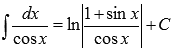, находящиеся в таблице первообразных.

Разберем первый случай, второй абсолютно аналогичен.

Воспользуемся методом подстановки:

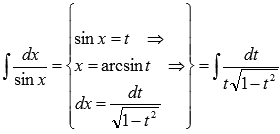
Пришли к задаче интегрирования иррациональной функции. Здесь нам также поможет метод подстановки:

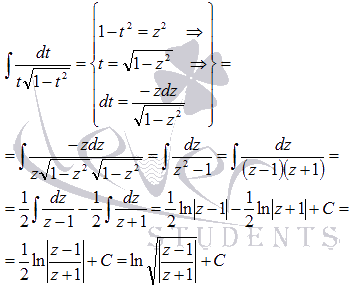
Осталось провести обратную замену 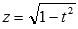и t = sinx:

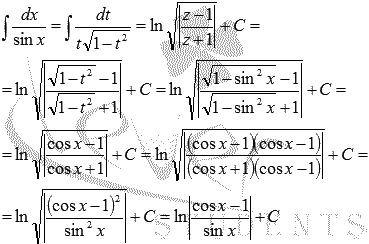
К началу страницы

· Отдельно хочется остановиться на интегралах, содержащих степени тригонометрических функций, вида .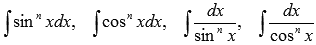

Подробно о принципах их нахождении можете ознакомиться в разделе интегрирование с использованием рекуррентных формул. Если изучите вывод этих формул, то без особого труда сможете брать интегралы вида 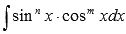, где m и n – натуральные числа.

К началу страницы

· Когда тригонометрические функции идут в комбинациях с многочленами или показательными функциями, то применяется метод интегрирования по частям. В этом разделе даны рекомендации для нахождения интегралов , .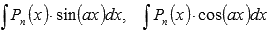

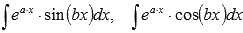К началу страницы

· Максимум творчества приходится вкладывать, когда подынтегральная функция содержит тригонометрические функции с различными аргументами.

Здесь на помощь приходят основные формулы тригонометрии. Так что выписывайте их на отдельный листочек и держите перед глазами.

Пример.

Найти множество первообразных функции .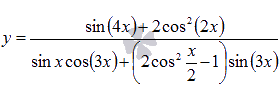

Решение.

Формулы понижения степени дают 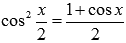и .

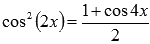Поэтому

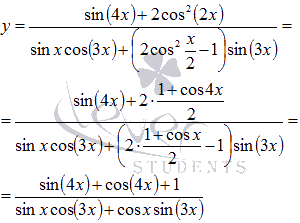
Знаменатель представляет собой формулу синуса суммы, следовательно,

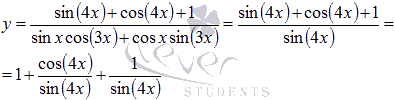
Приходим к сумме трех интегралов.

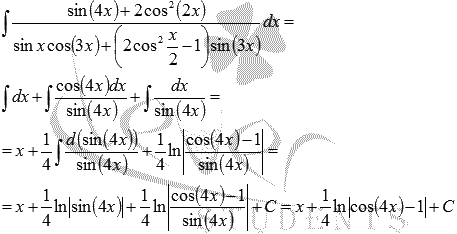
К началу страницы

· Подынтегральные выражения, содержащие тригонометрические функции, иногда можно свести к дробно рациональным выражениям, используя стандартную тригонометрическую подстановку.

Выпишем тригонометрические формулы, выражающие синус, косинус, тангенс через тангенс половинного аргумента:

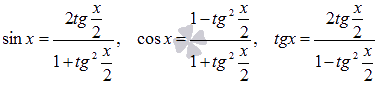
При интегрировании нам также понадобится выражение дифференциала dx через тангенс половинного угла.

Так как 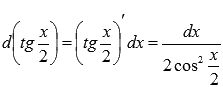, то

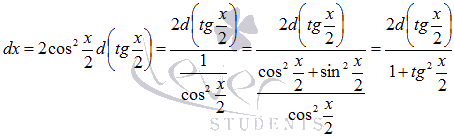
То есть, 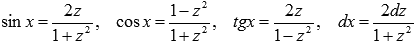, где .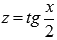

Пример.

Найти неопределенный интеграл .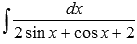

Решение.

Применим стандартную тригонометрическую подстановку:

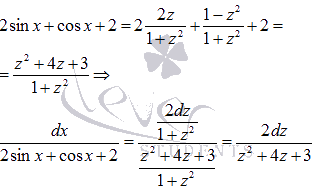
Таким образом, .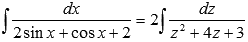

Разложение на простейшие дроби подынтегральной функции приводит нас к сумме двух интегралов:

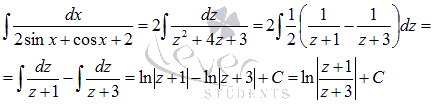
Осталось провести обратную замену :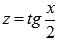

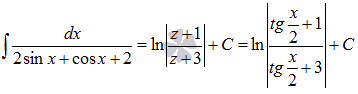
ЗАМЕЧАНИЕ:

Формулы, выражающие тригонометрические функции через тангенс их половинного аргумента, не являются тождествами. Поэтому, полученное выражение 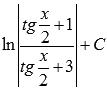является множеством первообразных функции 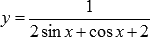только на области своего определения.

Дата добавления: 2014-01-15