Дисперсія дискретної випадкової величини, властивості

Математичне сподівання випадкової величини є середнім очікуваним значенням цієї величини, або є точкою на числовій осі, біля якої розкидані можливі значення випадкової величини. Але цього не досить для повної характеристики випадкової величини бо можливі значення випадкової величини більш або менш бувають розкидані біля математичного сподівання. Це явище називається розсіюванням випадкової величини. Так наприклад, дві випадкові величини 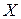і 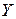мають однакові математичні сподівання. З цього прикладу ми бачимо, що можливі значення випадкової величини 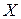більше розкидані (розсіяні)

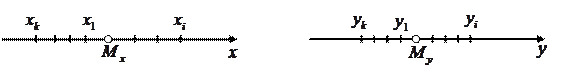
біля математичного сподівання 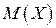ніж у випадкової величини 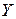. Для кількісної оцінки розсіювання можливих значень випадкової величини біля її математичного сподівання користуються числовими характеристиками випадкової величини, які називаються дисперсією і середнім квадратичним відхиленням. Ці величини і є мірою розсіювання можливих значень випадкової величини біля її математичного сподівання.

Дисперсія дорівнює математичному сподіванню квадрата відхилення випадкової величини від її математичного сподівання, яка позначається так:

,

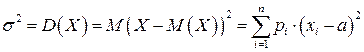де .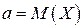

Для практичного обчислення дисперсії зручно користуватися другою формулою, яка отримується з попередньої формули:

.

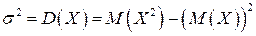Дата добавления: 2014-01-11