Распределение молекул по скоростям

Молекулы газа, находящегося в сосуде, двигаясь хаотически, непрерывно сталкиваются друг с другом и обмениваются энергией. В результате этого скорости молекул газа, который находится в равновесном состоянии, могут иметь самые разные значения – и очень большие, и близкие к нулю. Следовательно, скорость молекулы – непрерывная случайная величина. Но неправомерно ставить вопрос, какова вероятность того, что скорость молекулы равна, например, 150,75 м/с. Если бы была возможность одновременно и совершенно точно измерить скорости всех молекул в данном объеме газа, то среди них не нашлось бы молекулы точно с такой скоростью, но были бы молекулы, со скоростями, близкими к этому значению. Поэтому можно говорить лишь о вероятности того, что величина скорости молекулы лежит в некотором интервале скоростей . Эту вероятность можно определить так же, как это делалось в предыдущем примере с шарами: , где 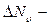число молекул, величина скорости которых лежит в интервале 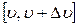, общее число молекул газа.

Отложим интервал возможных значений скорости на оси абсцисс. Разобьем весь интервал на отрезки шириной . На этих отрезках построим столбики, высота которых 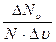представляет собой плотность вероятности 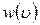нахождения молекул в интервале скоростей . Полученная столбчатая диаграмма называется гистограммой (рис. 8.2.1). Площадь каждого столбика равна , площадь всей гистограммы, в соответствии с условием нормировки, равна единице, что физически означает равенство единице полной вероятности нахождения молекул во все интервале скоростей от нуля до бесконечности.

В пределе при огибающая столбиков превращается в гладкую кривую (рис. 8.2.2), которую можно задать аналитически в виде функции , которая носит название функции распределения молекул по скоростям. Тогда вероятность того, что величина скорости молекул лежит в интервале , равна и определяется площадью заштрихованной фигуры. С другой стороны, равна относительному числу молекул, скорости которых лежат в указанном интервале: .

Полная площадь фигуры на рис. 8.2.2, ограниченной осями координат и кривой , имеет смысл полной вероятности и равна единице:

.

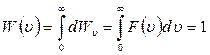Функция распределения молекул газа по абсолютным значениям скоростей была получена Максвеллом и является справедливой для идеального газа, состоящего из одинаковых частиц, находящегося в состоянии равновесия, в отсутствии внешних силовых полей. Аналитически функция задается следующим

выражением: , где 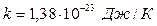(постоянная

Больцмана). Константа находится из условий нормировки: . Вычислив интеграл, получим выражение для константы: .

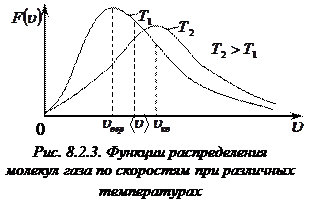С учетом этого результата функцию Максвелла – функцию распределения молекул газа по абсолютным значениям скоростей – можно записать в следующем виде:

.

При увеличении температуры максимум функции сдвигается в сторону больших значений скорости, при этом максимум становится ниже, поскольку площадь под кривой, в соответствии с условием нормировки, остается постоянной и равна единице (рис. 8.2.3).

Так как , где 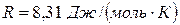(универсальная газовая постоянная), то функции распределения молекул по скоростям можно придать вид: . Умножив соответствующую вероятность на

полное число молекул газа , получим число молекул , модуль скорости которых лежит в интервале . Чтобы найти число молекул , модуль скорости которых лежит в пределах значений от до , необходимо провести интегрирование:

. (8.2.1)

Функция 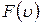имеет максимум при значении скорости

, (8.2.2)

которое вычисляется из условия и называется наиболее вероятной скоростью.

Средняя скорость молекул определяется по формуле:

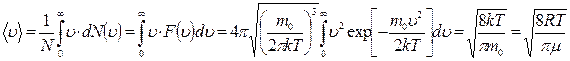.(8.2.3)

Среднее значение квадрата скорости 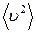найдем по формуле:

.

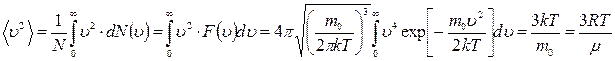Величина называется средней квадратичной скоростью и равна

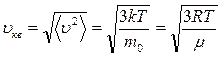. (8.2.4)

Исходя из распределения молекул по скоростям, можно найти распределение молекул газа по значениям кинетической энергии . Для этого перейдем от перемен-

ной к переменной . Подставив в функцию распределения и , получим .

Тогда средняя кинетическая энергия молекулы идеального газа

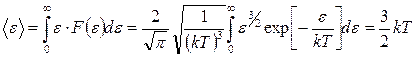. (8.2.5)

Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа. При , следовательно, при 0 К прекращается поступательное движение молекул газа и становится равным нулю давление газа на стенки сосуда.

Среднюю энергию поступательного движения молекулы газа можно найти, также используя среднюю квадратичную скорость:

. (8.2.6)

Пример 8.2.1. В некотором объеме газа содержится число молекул, равное . Рассматривая этот газ как идеальный, определить число молекул, скорости которых 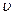меньше 0,001 наиболее вероятной скорости.

Решение:

Для решения этой задачи удобно воспользоваться распределением молекул по относительным скоростям. Пусть 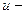относительная скорость, равная отношению абсолютной скорости 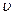к наиболее вероятной скорости :. Подставив в функцию распределения молекул по абсолютным значениям скорости и , получим функцию распределения молекул по относительным скоростям: . Тогда число молекул , относительные скорости которых заключены в пределах от до , определяется формулой .

Разложим экспоненту в ряд: . По условию задачи, максимальная скорость молекул , откуда 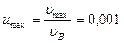. Для таких значений можно пренебречь всеми слагаемыми, кроме 1. Следовательно, 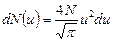. Интегрируя это выражение по скорости в пределах от 0 до , получим . Подставив в эту формулу значения всех величин и произведя вычисления, получим молекул.

Ответ: молекул.

Пример 8.2.2. Найти для кислорода при температуре наиболее вероятную, среднюю и среднюю квадратичную скорости молекул. Определить относительное число молекул 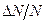, скорости которых отличаются от наиболее вероятной не более, чем на 2 %.

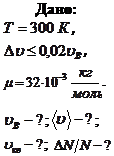
Решение:

Наиболее вероятная скорость по 8.2.2 .

Средняя скорость по 8.2.3 .

Средняя квадратичная скорость по 8.2.4 .

Интервал значений скорости молекул . Поэтому можно считать, что . Следовательно, .

С учетом того, что 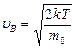, получим .

Ответ: , , , .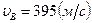

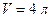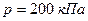Пример 8.2.3. Колба вместимостью содержит газ массой под давлением . Определить среднюю квадратичную скорость молекул газа.

Решение:

Средняя квадратичная скорость молекул идеального газа по 8.2.4 зависит от температуры . Давление газа связано с концентрацией его молекул по 7.4.2 соотношением , где 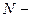количество молекул газа в сосуде. Учитывая, что , получим , откуда .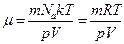

Подставим в формулу для средней квадратичной скорости

Ответ: .

Пример 8.2.4. Найти среднее число столкновений в единицу времени молекул азота при давлении и температуре . Эффективный диаметр молекулы азота .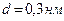

Решение:

Из уравнений(по 7.4.2) и 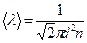(по 7.3.4) имеем 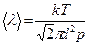. Среднее число столкновений , где .

Следовательно,

.

Ответ: .

Дата добавления: 2014-01-20