
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Явления переноса в термодинамически неравновесных системах
|
|
|
|
В МКТ равновесное состояние рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла. Любое неравновесное состояние газа всегда связано с нарушением полной хаотичности движения. Основной особенностью неравновесных состояний является стремление газа самопроизвольно переходить к равновесному состоянию. При этом возникают необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность ( обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение или динамическая вязкость (обусловлено переносом импульса). В каждом конкретном случае явления переноса определяются теми отклонениями от максвелловского распределения молекул по скоростям, которые имеют место в данном неравновесном состоянии. Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось Oz была ориентирована в направлении переноса.
1. Внутреннее трение (динамическая вязкость)
Предположим, что поток газа или жидкости движется параллельно неподвижной плоскости xOy, причем скорость упорядоченного движения газа 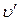 меняется от слоя к слою. Импульс каждой молекулы можно разложить на две составляющие, одна из которых обусловлена участием молекулы в хаотическом, другая – в упорядоченном движении. Если температура газа однородна, то при переходе молекул из одного слоя в другой составляющая импульса, обусловленная участием в хаотическом движении, не изменяется. Иначе обстоит дело с другой составляющей. Выде
меняется от слоя к слою. Импульс каждой молекулы можно разложить на две составляющие, одна из которых обусловлена участием молекулы в хаотическом, другая – в упорядоченном движении. Если температура газа однородна, то при переходе молекул из одного слоя в другой составляющая импульса, обусловленная участием в хаотическом движении, не изменяется. Иначе обстоит дело с другой составляющей. Выде лим в газе на границе двух слоёв площадку S, имеющую координату Z (рис. 8.4.1). Пролетающие через неё вследствие теплового хаотического движения молекулы из слоя с большей скоростью молекул в слой с меньшей скоростью имеют значительную составляющую импульса, обусловленную участием молекул в упорядоченном движении газа. Попав в более медленный слой, они сталкиваются с другими молекулами этого слоя и передают им избыток своего импульса, увеличивая тем самым скорость движения «медленного» слоя. Наоборот, молекулы, попадающие из слоя с меньшей скоростью упорядоченного движения в слой с большей скоростью, будут увеличивать свой импульс за счёт столкновения с молекулами этого слоя, и тем самым начнут тормозить его движение. Столкновение молекул происходит на расстоянии, равном, в среднем, длине свободного пробега
лим в газе на границе двух слоёв площадку S, имеющую координату Z (рис. 8.4.1). Пролетающие через неё вследствие теплового хаотического движения молекулы из слоя с большей скоростью молекул в слой с меньшей скоростью имеют значительную составляющую импульса, обусловленную участием молекул в упорядоченном движении газа. Попав в более медленный слой, они сталкиваются с другими молекулами этого слоя и передают им избыток своего импульса, увеличивая тем самым скорость движения «медленного» слоя. Наоборот, молекулы, попадающие из слоя с меньшей скоростью упорядоченного движения в слой с большей скоростью, будут увеличивать свой импульс за счёт столкновения с молекулами этого слоя, и тем самым начнут тормозить его движение. Столкновение молекул происходит на расстоянии, равном, в среднем, длине свободного пробега  от площадки S. Поэтому молекулам, пролетающим площадку снизу вверх, нужно приписать значение скорости газа в сечении с координатой
от площадки S. Поэтому молекулам, пролетающим площадку снизу вверх, нужно приписать значение скорости газа в сечении с координатой  , а молекулам, пролетающим сверху вниз, с координатой
, а молекулам, пролетающим сверху вниз, с координатой  .
.
Тогда вверх через площадку S из нижнего слоя одной молекулой в среднем пе-
реносится составляющая импульса 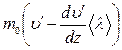 , а обратно
, а обратно  . Соответственно, из верхнего слоя вниз переносится составляющая импульса
. Соответственно, из верхнего слоя вниз переносится составляющая импульса  , а обратно
, а обратно 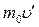 . Разность этих величин
. Разность этих величин 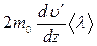 представляет собой изменение
представляет собой изменение
импульса слоя, рассчитанное на одну молекулу. Для того чтобы найти полное изменение импульса слоя, нужно эту величину умножить на число молекул, пролетающих площадку за время  .
.
Упрощённо это число можно подсчитать следующим образом. Рассмотрим параллелепипед с основанием S и высотой, равной средней скорости теплового движения молекул 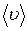 . Из всех находящихся в нём молекул за единицу времени пролетят через площадку S только те, скорость которых направлена к площадке. Поскольку все направления движения молекул равновероятны, то можно считать, что в вертикальном направлении движется 1/3 всех молекул, из них половина движется сверху вниз, а вторая половина – снизу вверх. Если плотность газа везде одинакова и в единице объёма газа содержится n молекул, то число их в объёме параллелепипеда равно
. Из всех находящихся в нём молекул за единицу времени пролетят через площадку S только те, скорость которых направлена к площадке. Поскольку все направления движения молекул равновероятны, то можно считать, что в вертикальном направлении движется 1/3 всех молекул, из них половина движется сверху вниз, а вторая половина – снизу вверх. Если плотность газа везде одинакова и в единице объёма газа содержится n молекул, то число их в объёме параллелепипеда равно  . Следовательно, через площадку S в единицу времени пролетит
. Следовательно, через площадку S в единицу времени пролетит  молекул, а за время
молекул, а за время  пролетит
пролетит  молекул. Таким образом, полное изменение импульса равно
молекул. Таким образом, полное изменение импульса равно  .
.
Так как изменение импульса тела равно импульсу действующей силы, следовательно,
 . (8.4.1)
. (8.4.1)
Это уравнение представляет собой закон Ньютона. Сила F, вызывающая торможение слоя, движущегося быстрее, называется силой внутреннего трения. Явление переноса импульса без переноса массы вещества при наличии градиента скорости движения слоев жидкости или газа, называется внутренним трением
(динамической вязкостью). Величина  называется коэффициентом динамической вязкости. Учитывая, что плотность газа
называется коэффициентом динамической вязкости. Учитывая, что плотность газа  , коэффициент динамической вязкости равен:
, коэффициент динамической вязкости равен:
 . (8.4.2)
. (8.4.2)
В векторной форме уравнение закона Ньютона может быть записано следующим образом:  , (8.4.3)
, (8.4.3)
где 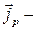 вектор плотности потока импульса. Модуль этого вектора равен
вектор плотности потока импульса. Модуль этого вектора равен  . Знак «–» показывает, что импульс переносится в направлении убывания скорости.
. Знак «–» показывает, что импульс переносится в направлении убывания скорости.
2. Теплопроводность
Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени, вследствие постоянных столкновений молекул, участвующих в тепловом хаотическом движении, происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, выравнивание температур. Перенос энергии в форме теплоты (без переноса массы) при наличии градиента температуры называется теплопроводностью.
 Предположим, что температура газа изменяется только в направлении оси Oz (рис. 8.4.2). Экспериментально установлено, что в этом случае теплопроводность газа определяется формулой Фурье:
Предположим, что температура газа изменяется только в направлении оси Oz (рис. 8.4.2). Экспериментально установлено, что в этом случае теплопроводность газа определяется формулой Фурье:
 , (8.4.4)
, (8.4.4)
где  количество теплоты, переносимое за время
количество теплоты, переносимое за время  через площадку S, расположенную перпендикулярно оси Oz;
через площадку S, расположенную перпендикулярно оси Oz;
 градиент температуры газа;
градиент температуры газа;  коэффициент теплопроводности,
коэффициент теплопроводности,
который зависит от свойств газа и тех условий, в которых находится газ.
В слое с бòльшей температурой молекулы газа имеют бòльшую кинетическую энергию, чем в слое с меньшей температурой. Попадая при хаотическом движении в этот слой, они при столкновениях с другими молекулами слоя передают им избыток своей энергии и тем самым увеличивают его температуру. Наоборот, молекулы, попадающие из слоя с меньшей температурой, в слой с бòльшей температурой, будут увеличивать в нем свою энергию за счет других молекул слоя и тем самым понижать его температуру. Поэтому в МКТ перенос количества теплоты  через площадку S рассматривается как перенос через эту площадку средней кинетической энергии хаотического движения молекул.
через площадку S рассматривается как перенос через эту площадку средней кинетической энергии хаотического движения молекул.
Из тех же соображений, что и при вычислении коэффициента динамической вязкости, молекулам, пролетающим площадку S снизу вверх, нужно приписать среднюю энергию, соответствующую температуре 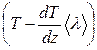 в плоскости
в плоскости  , а
, а
молекулам, летящим сверху вниз, – значение энергии, определяемое температурой
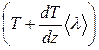 в плоскости
в плоскости  . Средняя кинетическая энергия молекулы газа связана с его температурой соотношением
. Средняя кинетическая энергия молекулы газа связана с его температурой соотношением  , поэтому вверх через площадку S из нижнего слоя одной молекулой переносится энергия
, поэтому вверх через площадку S из нижнего слоя одной молекулой переносится энергия 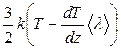 , а обратно
, а обратно  . Соответственно, из верхнего, более нагретого слоя, вниз переносится энергия
. Соответственно, из верхнего, более нагретого слоя, вниз переносится энергия 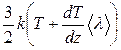 , а обратно
, а обратно  . Разность этих величин, равная
. Разность этих величин, равная  ,
,
представляет собой среднюю энергию, переносимую одной молекулой, перелетающей из слоя в слой.
Число молекул n в единице объема газа обратно пропорционально температуре Т, а средняя скорость молекул 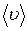 пропорциональна
пропорциональна 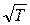 , поэтому произведение
, поэтому произведение  пропорционально
пропорционально  . Если разница температур слоев невелика, то можно считать, что
. Если разница температур слоев невелика, то можно считать, что  для обоих слоев приблизительно одинаково. Тогда, как и при вычислении коэффициента динамической вязкости, число молекул, пролетающих в одном направлении через площадку S в единицу времени, равно
для обоих слоев приблизительно одинаково. Тогда, как и при вычислении коэффициента динамической вязкости, число молекул, пролетающих в одном направлении через площадку S в единицу времени, равно 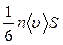 . Таким образом, через площадку S за время
. Таким образом, через площадку S за время  переносится энергия
переносится энергия
 . (8.4.5)
. (8.4.5)
Это уравнение представляет собой закон Фурье.
Сравнивая полученное выражение с эмпирической формулой, найдем коэффициент теплопроводности:
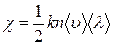 . (8.4.6)
. (8.4.6)
Примечание: это выражение можно преобразовать, введя удельную теплоемкость при постоянном объеме  , физический смысл которой будет раскрыт в 9.5. Поскольку
, физический смысл которой будет раскрыт в 9.5. Поскольку  есть, очевидно, средняя энергия молекул в единице объема газа, то количество теплоты, необходимое для нагревания единицы объема газа на один градус при постоянном объеме, равно
есть, очевидно, средняя энергия молекул в единице объема газа, то количество теплоты, необходимое для нагревания единицы объема газа на один градус при постоянном объеме, равно 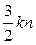 . Так как масса единицы объема газа равна его плотности
. Так как масса единицы объема газа равна его плотности 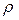 , то удельная теплоемкость газа
, то удельная теплоемкость газа  , откудаи
, откудаи  .
.
С учетом этого  . (8.4.6’)
. (8.4.6’)
В векторной форме уравнение закона Фурье может быть записано следующим
образом  , (8.4.7)
, (8.4.7)
где  вектор плотности теплового потока. Модуль этого вектора равен
вектор плотности теплового потока. Модуль этого вектора равен . Знак «–» показывает, что теплота переносится в направлении убывания температуры.
. Знак «–» показывает, что теплота переносится в направлении убывания температуры.
3. Диффузия
 Когда в смеси газов концентрация какого-либо газа распределена неравномерно, то возникает перенос этого газа в места с меньшей концентрацией. Перенос массы (без переноса энергии) при наличии градиента концентрации называется диффузией. Если в сосуде находится только один газ, плотность которого в занимаемом им объеме неодинакова, то происходит диффузия молекул газа в среде того же самого газа, т.е. самодиффузия.
Когда в смеси газов концентрация какого-либо газа распределена неравномерно, то возникает перенос этого газа в места с меньшей концентрацией. Перенос массы (без переноса энергии) при наличии градиента концентрации называется диффузией. Если в сосуде находится только один газ, плотность которого в занимаемом им объеме неодинакова, то происходит диффузия молекул газа в среде того же самого газа, т.е. самодиффузия.
Предположим, что плотность газа 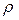 изменяется только в направлении оси Oz (рис. 8.4.3). Экспериментально установлено, что диффузия газа описывается формулой:
изменяется только в направлении оси Oz (рис. 8.4.3). Экспериментально установлено, что диффузия газа описывается формулой: , где
, где  масса газа, переносимая за время
масса газа, переносимая за время  через площадку S, расположенную перпендикулярно оси Oz;
через площадку S, расположенную перпендикулярно оси Oz;  градиент плотности газа;
градиент плотности газа; 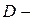 коэффициент диффузии, который зависит не только от природы диффундирующего газа и условий, в которых он находится, но и от природы среды, в которой он диффундирует, и условий, при которых находится эта среда.
коэффициент диффузии, который зависит не только от природы диффундирующего газа и условий, в которых он находится, но и от природы среды, в которой он диффундирует, и условий, при которых находится эта среда.
Рассмотрим самодиффузию газа и вычислим коэффициент диффузии. Обозначим через  и
и  среднее число молекул, содержащихся в объеме газа в сечениях
среднее число молекул, содержащихся в объеме газа в сечениях
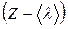 ,
, 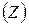 и
и  соответственно.
соответственно.
Очевидно, что 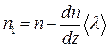 , а
, а  .
.
Можно считать, что в единицу времени через площадку S снизу вверх пролетят  молекул, а обратно
молекул, а обратно  молекул. Из верхнего слоя вниз через площадку пролетает
молекул. Из верхнего слоя вниз через площадку пролетает  молекул, а обратно
молекул, а обратно  молекул.
молекул.
Разность этих величин дает число  молекул, пролетающих через эту площадку в единицу времени в направлении снизу вверх:
молекул, пролетающих через эту площадку в единицу времени в направлении снизу вверх:
 .
.
Умножая  на массу одной молекулы
на массу одной молекулы  и на время
и на время  , найдем массу газа
, найдем массу газа
 , переносимого за время
, переносимого за время  через площадку S:
через площадку S:
 .
.
Так как  , то
, то
 . (8.4.8)
. (8.4.8)
Это уравнение представляет собой закон Фика.
Сравнивая полученное выражение с эмпирической формулой, найдем коэффициент диффузии:
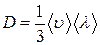 . (8.4.9)
. (8.4.9)
В векторной форме закон Фика может быть записан следующим образом:
 , (8.4.10)
, (8.4.10)
где  вектор плотности потока массы. Модуль этого вектора равен
вектор плотности потока массы. Модуль этого вектора равен  .
.
Знак «–» показывает, что масса переносится в направлении убывания плотности. Сравним явления переноса между собой.
Таблица 8.4.1.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2706; Нарушение авторских прав?; Мы поможем в написании вашей работы!