
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Явления переноса
|
|
|
|
| Явление | Переносимая величина | Уравнение переноса | Формула для коэффициента переноса |
| Динамическая вязкость (внутреннее трение) | Импульс | 
| 
|
| Теплопроводность | Энергия в форме теплоты | 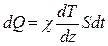
|  
|
| Диффузия | Масса | 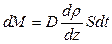
| 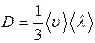
|
Закономерности всех явлений переноса сходны между собой, что обусловлено общностью лежащего в основе явлений внутреннего трения, теплопроводности и диффузии молекулярного механизма перемешивании молекул в процессе их хаотического движения и столкновений друг с другом.
Сравнивая выражения для коэффициентов переноса, получим следующие соотношения между ними:  и
и 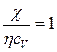 .
.
Все три коэффициента зависят от длины свободного пробега молекул  . Поэтому из опытов по диффузии, теплопроводности или внутреннему трению можно вычислить
. Поэтому из опытов по диффузии, теплопроводности или внутреннему трению можно вычислить  и подсчитать эффективное поперечное сечение молекул
и подсчитать эффективное поперечное сечение молекул  .
.
 Пример 8.4.1. Два тонкостенных коаксиальных цилиндра длиной
Пример 8.4.1. Два тонкостенных коаксиальных цилиндра длиной  могут свободно вращаться вокруг их общей оси. Радиус большого цилиндра R =5 см. Между цилиндрами имеется зазор
могут свободно вращаться вокруг их общей оси. Радиус большого цилиндра R =5 см. Между цилиндрами имеется зазор  . Оба цилиндра находятся в воздухе при нормальных условиях. Внутренний цилиндр приводят во вращение с постоянной частотой
. Оба цилиндра находятся в воздухе при нормальных условиях. Внутренний цилиндр приводят во вращение с постоянной частотой  . Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту
. Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту  . При расчетах изменением относительной скорости цилиндров пренебречь. Масса т внешнего цилиндра равна 100 г.
. При расчетах изменением относительной скорости цилиндров пренебречь. Масса т внешнего цилиндра равна 100 г.

 Решение:
Решение:
При вращении внутреннего цилиндра слой воздуха увлекается им и начинает участвовать во вращательном движении. Вблизи поверхности этого цилиндра слой воздуха приобретает со временем практически такую же линейную скорость, как и скорость точек на поверхности цилиндра, т.е.  . Т.к.
. Т.к.  , то приближенно можно считать
, то приближенно можно считать 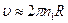 .
.
 Вследствие внутреннего трения момент импульса передается соседним слоям газа и, в конечном счете, внешнему цилиндру. За интервал времени
Вследствие внутреннего трения момент импульса передается соседним слоям газа и, в конечном счете, внешнему цилиндру. За интервал времени  внешний цилиндр приобретает момент импульса
внешний цилиндр приобретает момент импульса  , где
, где 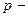 импульс, полученный за
импульс, полученный за  внешним цилиндром. Отсюда
внешним цилиндром. Отсюда 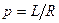 .
.
С другой стороны, 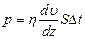 , где
, где  динамическая вязкость;
динамическая вязкость; 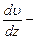 градиент скорости;
градиент скорости;  площадь поверхности цилиндра
площадь поверхности цилиндра 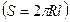 . Приравняв правые части полученных уравнений
. Приравняв правые части полученных уравнений 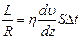 , выразим искомый интервал времени:
, выразим искомый интервал времени: 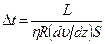 (1).
(1).
Найдем входящие в эту формулу величины 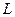 ,
, 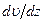 , и
, и 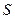 . Момент импульса
. Момент импульса  , где
, где 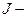 момент инерции цилиндра
момент инерции цилиндра  ; т – его масса;
; т – его масса;  угловая скорость внешнего цилиндра
угловая скорость внешнего цилиндра 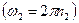 . С учетом этого запишем
. С учетом этого запишем 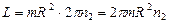 . Градиент скорости
. Градиент скорости 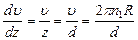 .
.
Подставим в выражение найденные величины и получим  .
.
Динамическая вязкость воздуха, найденная по таблице, 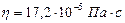 .
.
Следовательно, 
Ответ: 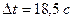 .
.
Пример 8.4.2. Покрытие парового котла состоит из двух слоев теплоизоляции. Толщина и коэффициент теплопроводности каждого слоя равны, соответственно,  ,
,  ,
, 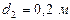 ,
, . Определить температуру t2 на границе между слоями, если температура наружных поверхностей t1= 8000 C и t3= 600 C. Найти эквивалентный коэффициент теплопроводности такого материала, из которого можно сделать однослойное покрытие прежней толщины.
. Определить температуру t2 на границе между слоями, если температура наружных поверхностей t1= 8000 C и t3= 600 C. Найти эквивалентный коэффициент теплопроводности такого материала, из которого можно сделать однослойное покрытие прежней толщины.
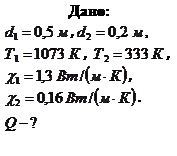
 Решение:
Решение:
В соответствии с законом Фурье тепловые потоки (количество теплоты, переносимое через единицу площади в единицу времени) через первый и второй слои покрытия равны:


 и
и 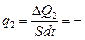
 .
.
Так как тепловой поток не может прерываться внутри покрытия, то 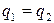 .
.
Приравнивая тепловые потоки, находим после преобразования температуру T2:
 .
.
Для нахождения эквивалентного коэффициента теплопроводности  однослойного покрытия толщиной
однослойного покрытия толщиной 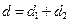 запишем закон Фурье в виде:
запишем закон Фурье в виде: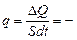
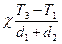 .
.
Разность температур 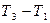 представим в виде:
представим в виде:  .
.
Подставляя разности температур, выраженные через соответствующие тепловые потоки 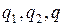 и учитывая условие непрерывности теплового потока
и учитывая условие непрерывности теплового потока  , получим:
, получим:  , откуда:
, откуда: 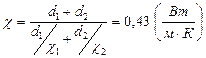 .
.
Ответ: 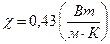 ,
, 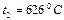 .
.
Пример 8.4.3. Какое количество теплоты Q теряет помещение за время  через окно за счет теплопроводности воздуха, заключенного между рамами? Площадь каждой рамы
через окно за счет теплопроводности воздуха, заключенного между рамами? Площадь каждой рамы 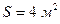 , расстояние между ними
, расстояние между ними 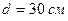 , температура помещения
, температура помещения  , температура наружного воздуха
, температура наружного воздуха  . Диаметр молекул воздуха
. Диаметр молекул воздуха  . Температуру воздуха между рамами считать равной среднему арифметическому температур помещения и наружного воздуха. Давление
. Температуру воздуха между рамами считать равной среднему арифметическому температур помещения и наружного воздуха. Давление 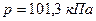 .
.

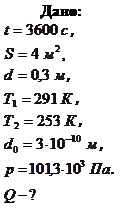 Решение:
Решение:
 Количество теплоты, перенесенное через площадку S за время
Количество теплоты, перенесенное через площадку S за время 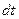 , определяется законом Фурье:
, определяется законом Фурье:  , где
, где  коэффициент теплопроводности воздуха. Учтем, что
коэффициент теплопроводности воздуха. Учтем, что 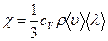 (1), где
(1), где  (2);
(2); 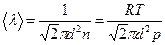 (3);
(3);  (4). Подставляя (2) – (4) в (1), получим
(4). Подставляя (2) – (4) в (1), получим 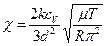 .
.
Здесь  – температура воздуха между рамами, удельная теплоемкость воздуха
– температура воздуха между рамами, удельная теплоемкость воздуха  , молярная масса воздуха
, молярная масса воздуха 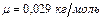 . Подставив числовые данные, найдем
. Подставив числовые данные, найдем 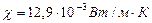 .
.
Учитывая, что 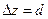 , имеем
, имеем 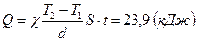 .
.
Ответ: 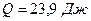 .
.

Глава 9. Основы классической термодинамики
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 580; Нарушение авторских прав?; Мы поможем в написании вашей работы!