Примеры инверсного кода

Информационные символы k	Контрольные символы m	Инверсный код n =k + m

Декодирование инверсного кода при его приёме осуществляется в два этапа. На первом этапе суммируются единицы в первой половине полной кодовой комбинации. Если сумма единицчётная, то контрольные символы т принимаются без изменений, если нечётная, то символы т инвертируются.

На втором этапе контрольные символы т сравниваются с символами k, и при наличии хотя бы одного несовпадения вся переданная комбинация п = k + m элементов бракуется. Это поэлементное сравнение эквивалентно суммированию по модулю 2. При отсутствии ошибок в обеих половинах символов полной кодовой комбинации их сумма равна нулю.

Пусть передана первая комбинация из табл. 4.12. Ниже показано суммирование для трёх вариантов приема переданной комбинации:

1) 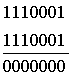2) 3)

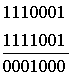
В первом варианте искажений нет и число единиц в информационных символах k четное, поэтому производится суммирование по модулю 2 с неинвертируемыми символами т,что в результате дает нулевую сумму. Во втором варианте число единиц в символах k нечётное, единица в пятом разряде искажена, и символы т инвертированы. В третьем варианте искажение возникло в четвертом разряде группы т. Таким образом, из трех вариантов лишь первый оказался без искажений, а второй и третий должны быть забракованы из-за наличия несовпадения в группах символов k и m.

Корректирующие возможности инверсного кода достаточно велики. Этому способствует метод его построения. Добавление т символов приводит к увеличению минимального кодового расстояния.

После инвертирования корректирующие возможности кода изменяются в зависимости от числа разрядов исходного двоичного кода. Так, если передаются все комбинации обычного двоичного кода с k = 2 (00, 01, 10 и 11), то этот непомехоустойчивый код, превращаясь в инверсный (0000, 0110, 1001 и 1111), увеличивает минимальное кодовое расстояние до d_min =2и позволяет обнаруживать все одиночные ошибки и 67% двойных ошибок.

Действительно, в каждой комбинации может быть С ₄² = 6 двойных ошибок: так, комбинация 0000 при двойных ошибках примет вид 1100, 0110, 0011, 1001, 1010 и 0101. При этом только второе и четвертое искажения не могут быть обнаружены.

У трёхразрядного двоичного кода (000, 001,.., 111) после преобразования его в инверсный код кодовое расстояние увеличивается до d_min =3. Это значит, что такой код гарантированно обнаруживает все двойные ошибки. Кроме того, он обнаруживает 80% тройных и четверных ошибок и все пяти- и шестикратные ошибки.

Четырехразрядный двоичный код (0000, 0001,.... 1111) после преобразования его в инверсный код имеет d_min = 4. Он обнаруживает все ошибки во втором, третьем, пятом, шестом и седьмом символах, не обнаруживает 22% четырехкратных ошибок и совсем не обнаруживает восьмикратные ошибки.

Высокие корректирующие возможности инверсного кода достигаются за счет очень большой избыточности. В этом отношении инверсный код значительно уступает другим кодам, о которых будет сказано далее.

4.7. КОДЫ С ОБНАРУЖЕНИЕМ
И ИСПРАВЛЕНИЕМ ОШИБОК

Если кодовые комбинации составлены так, что отличаются друг от друга на кодовое расстояние d = 3, то они образуют корректирующий код, который позволяет по имеющейся в кодовой комбинации избыточности не только обнаруживать, но и исправлять ошибки.

4.7.1. Коды Хэмминга

Для построения кода Хэмминга используется информационная часть в виде двоичного кода на все сочетания с числом информационных символов k, к которой добавляют контрольные символы т. Таким образом, общая длина полной кодовой комбинации n =k + m.

Рассмотрим последовательность кодирования и декодирования по Хэммингу.

Кодирование кодом Хэмминга предусматривает выполнение следующих этапов.

1. Определение числа контрольных символов. Для этого можно воспользоваться следующими рассуждениями. При передаче по каналу с помехами при единичном искажении может быть искажен любой из п символов кода, всего будет n вариантов искажённых комбинаций. Код может быть передан и без искажений. Таким образом, при единичном искажении может быть n + 1 вариантов передачи, включая передачу без искажений. Используя контрольные символы, необходимо различить все п + 1 вариантов. С помощью контрольных символов m можно описать 2 ^m событий. Значит, должно быть выполнено условие

2^m ≥ n + 1=k + m + 1. (4.3)

В неравенстве (4.3) по известной величине k находится число контрольных разрядов m, необходимых для построения кода, способного обнаружить и исправить заданное число ошибок.

В табл. 4.13 представлена зависимость между k и т,полученная из неравенства (4.3).

Таблица 4.13

Дата добавления: 2014-01-20