Пример 4.1. Закодировать кодом Хэмминга, исправляющим одну ошибку, информационную комбинацию двоичного кода 1101

Закодировать кодом Хэмминга, исправляющим одну ошибку, информационную комбинацию двоичного кода 1101.

В информационной комбинации содержится четыре информационных разряда, т.е. k =4.

Согласно табл. 4.13 число контрольных символов m =3, и в соответствии с (4.6) размещаются они на позициях 1, 2 и 4, а информационные символы – на позициях 3, 5, 6 и 7 полной кодовой комбинации, в которой всего семь разрядов, так как n=k+m. Символы информационной части известны, а контрольные символы необходимо определить.

Полную кодовую комбинацию можно записать в виде:

т ₁ m ₂ k ₄ m ₃ k ₃ k ₂ k ₁

?? 1?1 0 1

Для определения контрольных символов заполняем табл. 4.15 значениями информационных символов и в полученной таким образом табл. 4.16 суммируем по модулю 2 информационные символы каждой строки.

Таблица 4.16

Проверочная таблица кода Хэмминга,
заполненная информационными символами

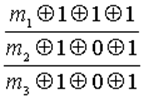
Очевидно, что суммирование информационных символов первой строки даёт 1, суммирование этих символов второй и третьей строк даёт 0. Следовательно, имеем следующий состав контрольных символов: т₁ = 1, m₂ =0, m₃ =0.

Подставляя контрольные символы на их позиции в (4.6), получим полную кодовую комбинацию кода Хэмминга: 1 0 1 0 1 0 1.

Декодирование кода Хэмминга. Для обнаружения и исправления ошибки выполняются следующие действия.

1. Заполнение проверочной таблицы символами полной кодовой комбинации

Проверочная таблица кода Хэмминга (см. табл. 4.15) заполняется символами полной кодовой комбинации с использованием структуры (4.6) этой комбинации.

2. Суммирование по модулю 2 строк проверочной таблицы

Символы всех строк проверочной таблицы суммируются по модулю 2. Если результат суммирования по всем строкам нулевой, то в принятой комбинации искажений нет. Наличие ненулевого результата означает наличие искажений.

3. Определение места искажения

Место искажения определяется двоичным числом, являющимся результатом суммирования. Для этого столбец результата суммирования читается по вертикали снизу вверх, так что старшим разрядом двоичного числа является результат суммирования последней строки проверочной таблицы, а младшим разрядом – результат суммирования первой строки проверочной таблицы.

4. Исправление искажения

Для исправления искажения полученное двоичное число переводят в десятичное, которое означает номер разряда полной кодовой комбинации, включая контрольные разряды, в котором имеется искажение. Счёт разрядов ведётся слева направо. Принятый символ этого разряда заменяется противоположным, т.е. 0 заменяется на 1 или 1 заменяется на 0. Получается неискажённая кодовая комбинация.

Контрольные символы в соответствии с (4.6) отбрасываются, неискажённая информационная часть обрабатывается.

Дата добавления: 2014-01-20