
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Одновременно совершаются гармонические колебания одного направления
|
|
|
|
Сложение колебаний.
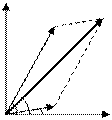 Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система участвует в нескольких колебательных процессах.
Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система участвует в нескольких колебательных процессах.
Предельные случаи:
1) Одинаковой частоты: 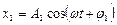 и
и 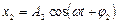 , то результирующее колебание
, то результирующее колебание 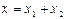 совершается с той же частотой по гармоническому закону
совершается с той же частотой по гармоническому закону 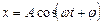 .
.
Опр. 2.4.1. Два гармонических колебательных процесса называются когерентными колебаниями, если они согласованно протекают во времени, так что их разность фаз остается постоянной.
Для отыскания 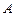 и
и 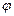 пользуются методом векторных диаграмм, основанный на том, что в каждый момент времени вращающиеся векторы амплитуд складываемых колебаний и результирующий вектор связаны соотношением
пользуются методом векторных диаграмм, основанный на том, что в каждый момент времени вращающиеся векторы амплитуд складываемых колебаний и результирующий вектор связаны соотношением 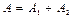 . В скалярной форме
. В скалярной форме 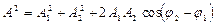 .
.
 Т.к. косинус – функция ограниченная, то возможные значения амплитуды заключе-ны в пределах
Т.к. косинус – функция ограниченная, то возможные значения амплитуды заключе-ны в пределах 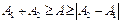
Начальная фаза результирующего колебания может быть найдена по формуле: 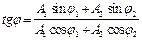 .
.
Частные случаи:
o 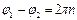 , где
, где  . Тогда
. Тогда 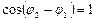 и
и 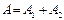
o 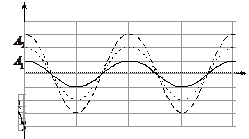
 , где
, где 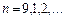 . Тогда
. Тогда 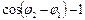 и
и 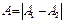
2) Разной частоты: 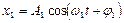 и
и 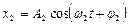 , то результирующее колебание не является гармоническим. Его можно представить в следующей форме:
, то результирующее колебание не является гармоническим. Его можно представить в следующей форме: 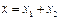
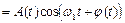 , где
, где 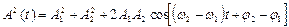 .
.
Начальная фаза 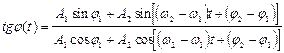 . Гармонические колебания, частоты которых различны, некогерентны, т.к. разность их фаз непрерывно изменяется с течением времени.
. Гармонические колебания, частоты которых различны, некогерентны, т.к. разность их фаз непрерывно изменяется с течением времени.
3) Мало отличаются по частоте – биения. Величина 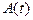 периодически изменяется в пределах от
периодически изменяется в пределах от 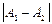 до
до 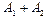 .
. 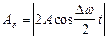 . Период биения
. Период биения 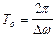 .
.
Частота биений 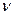 , возникающих при сложении двух колебаний с различными, но по значению частотами
, возникающих при сложении двух колебаний с различными, но по значению частотами 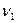 и
и 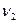 :
: 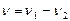 .
.
4) Сложное (негармоническое) периодическое колебание: в виде ряда Фурье.
2. Одновременно совершаются гармонические колебания во взаимно перпендикулярных направлениях вдоль осей x и y.
1) Одинаковой частоты: 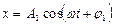 и
и 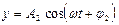 . Уравнение траектории результирующего колебания находится с помощью исключения из уравнений параметра t.
. Уравнение траектории результирующего колебания находится с помощью исключения из уравнений параметра t. 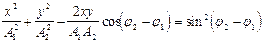 . Это уравнение эллипса, характеристики которого определяются значением разности фаз
. Это уравнение эллипса, характеристики которого определяются значением разности фаз 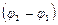 . В предельных случаях эллипс вырождается в прямую или окружность. В случае, если начальные фазы
. В предельных случаях эллипс вырождается в прямую или окружность. В случае, если начальные фазы 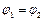 , уравнение траектории принимает вид:
, уравнение траектории принимает вид:  .
.
2) Разной частоты: замкнутые траектории, прочерчиваемые точкой называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.
Пример 2.4.1. Совершаются два колебания одинакового направления, выражаемых уравнениями 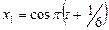 см, и
см, и 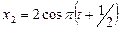 см. Определить амплитуды, периоды и начальные фазы складываемых колебаний. Написать уравнение результирующего колебания.
см. Определить амплитуды, периоды и начальные фазы складываемых колебаний. Написать уравнение результирующего колебания.
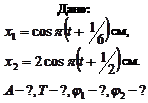
 Решение:
Решение:
 Уравнение гармонических колебаний в общем виде:
Уравнение гармонических колебаний в общем виде: 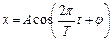 , тогда
, тогда 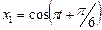 и
и 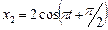 . Амплитуда результирующего колебания
. Амплитуда результирующего колебания 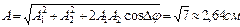 , т.к.
, т.к. 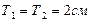 , то результирующее колебание будет иметь тот же период
, то результирующее колебание будет иметь тот же период 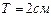 . Тангенс начальной фазы результирующего колебания
. Тангенс начальной фазы результирующего колебания 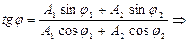
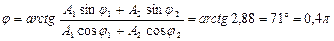 рад. Получаем уравнение результирующего колебания
рад. Получаем уравнение результирующего колебания 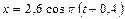 .
.
 Пример 2.4.2. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых
Пример 2.4.2. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых 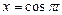 см и
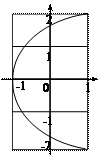
см и 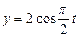 см. Определить траекторию точки. Построить траекторию с соблюдением масштаба.
см. Определить траекторию точки. Построить траекторию с соблюдением масштаба.
Решение:
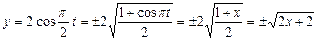 (т.к.
(т.к. 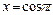 ). Мы получили уравнение параболы, ось которой лежит на оси
). Мы получили уравнение параболы, ось которой лежит на оси 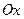 . Амплитуда колебаний по
. Амплитуда колебаний по 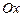 равна 1, по
равна 1, по 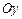 - 2. Период колебаний по
- 2. Период колебаний по 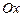 равен 2с, по
равен 2с, по 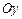 - 4с, т.е. в начальный момент времени имеем:
- 4с, т.е. в начальный момент времени имеем: 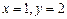
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 821; Нарушение авторских прав?; Мы поможем в написании вашей работы!