Затухающие колебания

Свободные затухающие колебания.

Если колебательная система выведена из положения равновесия и затем предоставлена самой себе, то она совершает колебания с частотой, зависящей от свойств системы. Колебания, которые совершает система (тело) после того, как она каким-либо образом выведена из устойчивого равновесия и затем предоставлена самой себе, называются свободными.

Опр. 2.5.1 Колебания наз. свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Опр. 2.5.2 Если свободные механические колебания происходят без потерь энергии, то они называются собственными колебаниями, а их частота – частотой собственных колебаний.

При наличии сил трения свободные колебания будут затухающими; их амплитуда непрерывно уменьшается вследствие потерь энергии. При наличии сопротивления период колебаний увеличивается, а если сопротивление достаточно велико (большая вязкость среды), движение перестает быть периодическим, это явление используется для демпфирования (гашения) нежелательных колебаний.

Опр. 2.5.3 Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.

Дифференциальное уравнение свободных затухающих колебаний: 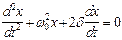, где колеблющаяся величина, описывающая тот или иной физический процесс; 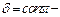коэффициент затухания, 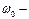циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при 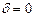(при отсутствии потерь энергии) наз. собственной частотой колебательной системы.

При малом затухании 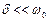общее решение дифференциального уравнения имеет вид: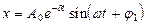или - уравнение затухающих колебаний (в среде, где сила сопротивления пропорциональна первой степени скорости), гдеамплитуда колебаний в момент времени 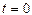, 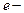основание натуральных логарифмов: 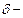коэффициент затухания. Величину 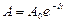называют амплитудой затухающих колебаний.

Промежуток времени 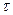, в течение которого амплитуда затухающих колебаний уменьшается в 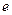раз, называется временем релаксации. .

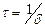Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (минимумами) колеблющейся физической величины. Тогда период (условный период) .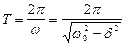

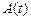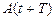Если и - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение 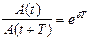называется декрементом затухания, а его логарифм 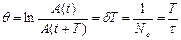- логарифмическим декрементом затухания – постоянная для данной колебательной системы величина – количественная характеристика быстроты убывания амплитуды затухающих колебаний, величина безразмерная; число колебаний, совершаемых за время уменьшения амплитуды в 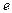раз. и .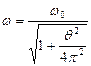

Опр. 2.5.4. Добротность (при малых значениях логарифмического декремента) .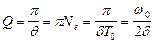

Добротностью колебательной системы называется безразмерная величина , равная произведению на отношение энергии 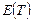колебаний системы в произвольный момент времени 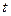к убыли этой энергии за промежуток времени от 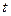до 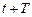, т.е. за один условный период затухающих колебаний:

Механическая энергия системы при затухающих колебаниях убывает со временем по закону 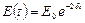, т.е. не сохраняется; часть ее переходит в тепло (диссипирует).

Пример 2.5.1. Амплитуда затухающих колебаний за время 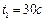уменьшилась в два раза. Во сколько раз она уменьшится за время ?

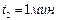Решение:

Имеем 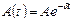. По условию задачи 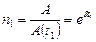. Отсюда 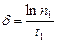. Подставляя это значение 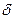в исходную формулу, получим 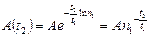. Откуда .

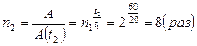Пример 2.5.2. Тело массой 5г совершает затухающие колебания. Через время 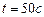тело потеряло 60% своей энергии. Определить коэффициент сопротивления среды.

Решение:

Потеря энергии телом 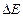будет равна 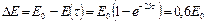, откуда 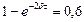или , т.е. 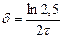. Коэффициент сопротивления среды 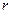определяется по формуле .

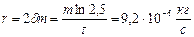Пример 2.5.3. Гиря массой 0,5 кг подвешена к пружине, жесткость которой 32 Н/м и совершает затухающие колебания. Определить их период, если 1) за время, в течение которого произошло 88 колебаний, амплитуда уменьшилась в 2 раза; 2) за время двух колебаний амплитуда уменьшилась в 20 раз.

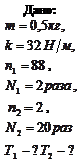Решение:

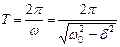, собственная циклическая частота 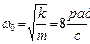. Коэффициент затухания 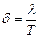, где 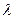находится из уравнения 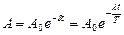. По условию 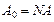, 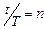. Тогда и 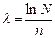, получаем 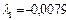; 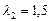. . 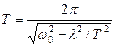Решая квадратное уравнение получим 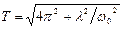и ,

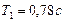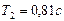
Свободные затухающие колебания (при 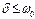) пружинного маятника: сила трения 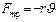, 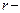коэффициент сопротивления. Циклическая частота: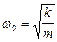. Коэффициент затухания 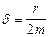. Добротность .

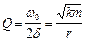Дата добавления: 2014-01-11