Принцип максимума Понтрягина

Соотношения выполняющиеся на оптимальном процессе, с учётом ограничений в постановке задачи (нет ограничений на состояние, независимость множества допустимых управлений от состояния) позволили определить необходимые условия оптимальности процесса (x*(t), u*(t)).

Полученные соотношения могут быть использованы для “сужения” исходного множества М допустимых процессов путём выделения из него только тех процессов, которые удовлетворяют необходимым условиям.

Совокупность приведённых условий, как правило, даёт возможность выделить единственную траекторию x*(t) из множества допустимых. Если при этом ещё известно (например из содержательной постановки задач) о существовании оптимальной траектории, то тем самым x*(t) и отвечающее ему управление u*(t) и есть решение задачи оптимального управления.

Комплекс условий, которому должен удовлетворять оптимальный процесс, называется принципом максимума Понтрягина. И его можно сформулировать в виде теоремы.

Теорема.

Пусть (x*(t), u*(t)) – оптимальный процесс в задаче оптимального управления (5-7). Тогда существует вектор функция y(t)= (y₁(t), y₂(t), …, y_n(t)), удовлетворяющая вместе с данным процессом следующим условиям:

1. Функция 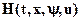достигает максимума значения по u при x=x*(t), y(t) на значении u=u*(t) при всех tÎ[0;T] (10)
2. Переменные y(t) удовлетворяют системе дифференциальных уравнений

i=1, 2, …, n,

1. В конечный момент времени t=T оптимальная траектория удовлетворяет условиям

i=m+1, m+2, …, n,

где m - переменные

Таким образом, система управлений может быть записана в форме

;

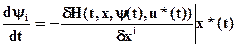i=1, 2, …, n.

Тема 13. Задача Эйлера вариационного исчисления.

Это первая задача в вариационном исчислении, методы и алгоритмы решения которой способствовали созданию ТОУ. Она имеет историческую значимость.

Задачей Эйлера в современном изложении называют задачу о минимуме функционала

(1)

при наличии ограничения

(2)

и граничных условий

x(0)=x₀; x(T)=x₁ (3)

где

а) xÎRⁿ – n –мерный вектор состояния

б) uÎRⁿ – n –мерный вектор управления (в данном случае размерность а и б одинакова

в) x₀; x₁ – заданные n –мерные вектора начального и конечного состояния системы

г) Rⁿ – символ n –мерного действительного пространства (метрическое пространство, изометричное конечному вещественному пространству Rⁿ)

Помимо векторных уравнений процесса (2) на элементы V(t)= (x(t), u(t)) допустимого множества М наложены ограничения:

x(t) – непрерывная и дифференцируемая

u(t) – непрерывная вектор – функции.

Функция - непрерывная и дифференцируемая по всем аргументам.

Ограничимся частным случаем n=1, на состояние и управление ограничений нет, т.е., 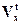и 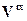, совпадают с числовыми осями X и U, а при t=0 и t=T представляют собой заданные точки х₀ и х₁

Свойства решения задачи Эйлера в значительной степени определяется характером индикатрисы (характер графического отображения, зависимости характеристик), т.е., подынтегрального выражения от управления u при фиксированных значениях x и t. Эту зависимость необходимо положить в основу классификации решений.

Случаи:

1. Постоянная индикатриса, т.е.,

=

2. Индикатриса с ограниченной нелинейностью по управлению.

3. Выпуклая 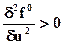, её исследование можно провести с помощью принципа максимума. В соответствии с принципом необходимо построить функцию Гамильтона.

т.к., ограничений на построение x и u нет, то применим необходимое условие максимума функции Гамильтона.

отсюда получаем

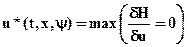(4)

система уравнения процесса и сопряжённое уравнение, используя ограничение (2)

(5)

Решая систему двух дифференциальных уравнений 2 и 5 относительно искомых переменных х и y, с учётом выражения 4 получаем процесс, удовлетворяющий необходимым условиям.

Дата добавления: 2014-01-20