Идея, основные элементы уравнения Беллмана

Тема 14. Уравнение Беллмана.

При постановке задачи ТОУ предполагалось, что такие элементы, как начальное состояние и начальный момент t, фиксированы. Но это не всегда выполняется на практике. При решении конкретной задачи оказывается удобным рассматривать её в составе множества качественно однотипных задач, описываемых теми же уравнениями процесса и функционалом, но с различными значениями перечисленных параметров.

Определяя оптимальное управление сразу для всего множества таких задач, получим решение в форме синтеза, которое будет представлять зависимость качественных свойств оптимального управления от состояния системы и текущего момента времени. Из этой задачи нетрудно получить решение для любых фиксированных начальных условий в обычной форме, т.е. найти оптимальное управление как функцию времени.

Решение подобных задач обладает рядом преимуществ. Главное из них состоит в том, что имеется полная информация об оптимальном управлении. Если при этом реализовались заранее неизвестные значения состояния системы, а на практике это типичная ситуация, то значение синтеза оптимального управления позволяет принять оптимальное решение в данной ситуации.

Поиск синтеза оптимального управления, т.е. совокупности качественно однородных свойств системы, – это более трудоемкая процедура по сравнению с решением обычной задачи оптимального управления.

С математической точки зрения отыскания синтеза оптимального управления сводится к решению нелинейного дифференциального уравнения с частными производными, называемого уравнением Гамильтона – Якоби – Беллмана (для непрерывных процессов). Сложность численного решения этого уравнения сильно возрастает с увеличением размерности решаемой задачи. Для дискретных процессов это менее сложно.

По исследованию операции представление о преемственности метода лишь к дискретным процессам.

Рассмотрим задачи оптимального управления с условием:

(1)

(2)

х(0)=х₀; uÎV^tх (3)

Из условий видно что отсутствуют ограничения на состояние, а множества допустимых управлений V^tх в отличие от принципа максимума (uÎV^t) не зависит от состояния х.

Т.е. множество 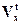при всех tÎ[0;T] совпадает с пространством х, а при t=0 задано начальное условие – фиксированная точка х₀. Ограничения на состояние х в момент t=T не задан.

Для получения уравнения Гамильтона – Якоби – Беллмана необходимо воспользоваться теоремой о достаточных условиях оптимальности, согласно которой если есть допустимый процесс

V*= (x*(t), u*(t))ÎМ и непрерывно дифференцируемая функция j(t, x) такие что при всех t, x

R(t, x*(t), u*(t))= 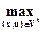R(t, x, u), tÎ[0;T]

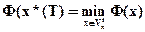при t=T

то процесс (x*(t), u*(t)) оптимален, т.е.,

õ(x*, u*)=

Известно, что

Ф(х)=j(Т,х) + F(х)

Введём функцию:

Р(t,х) = max R(t, x, u)

(заданная и непрерывная функция) предположим, что удалось так определить функцию j(Т,х) что

Р(t,х) =с(t)

с(t) – произвольное число, которое м.б. равно 0.

Ф(х)=с₁

Т.к. функция j(t, x) задана, следовательно задана и функция R(t, x, u) максимизируя которую по управлению uÎV^tх, найдём u*(t, x):

u*(t, x)= 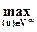R(t, x, u)

u*(t,x) является синтезом оптимального управления, решением рассматриваемой оптимизационной задачи. Для определения оптимального состояния вектора x*(t) подставим синтез от управлений u*(t, x) в уравнение процесса

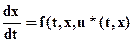х(0)=x₀ (4)

Определение оптимального состояния x*(t) сводится к решению задачи Коши (4) для уравнения процесса, замкнутого синтезом оптимальных управлений с начальными условиями х(0)= x₀

В отличие от синтеза оптимального управления u*(t, x) функцию

(5)

называют оптимальной программой управления.

Данное определение отражает, что оптимальная программа управления (ОПУ), определяемая формулой (5) отвечает уже не произвольному состоянию х, а конкретному оптимальному х*(t).

Изложенный метод нахождения процесса (х*(t); u*(t)), при априорных [5] ограничениях наложенных на функцию j(t,x), называется методом Гамильтона – Якоби – Беллмана. В этом случае процесс х*(t), u*(t) является оптимальным.

Дата добавления: 2014-01-20