Тепловые свойства твердых тел

Лекция № 15

Классическая теория теплоемкости твердых тел

Узлы кристаллической решетки кристаллов непрерывно колеблются около своих средних положений. Интенсивность колебаний возрастает с ростом температуры.

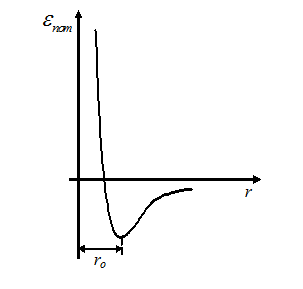Взаимодействие между частицами в кристалле может быть представлено потенциальной кривой.

В равновесном состоянии распо-ложение частиц в кристалле соответствует минимуму их ε_пот. При смещении от положения равновесия (например, при возрастании температуры) возникает сила, возвращающая ее обратно и частица начинает колебаться.

На каждую колебательную степень свободы приходится энергия равная kΤ ( 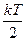на W_кин и 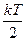на W_пот).

На каждый атом - 3kΤ.

На один киломоль - 3kΤN_a, то есть , , 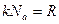где N_a – число Авогадро.

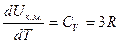
Поскольку объем твердых тел при нагревании мало изменяется, то

.

Следовательно, имеем - закон Дюлонга - Пти.

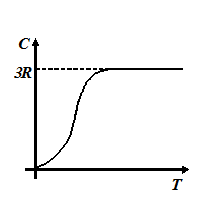
Молярная теплоемкость всех химически простых тел в кристаллическом состоянии одинакова и равна 3R (R – универсальная газовая постоянная).

Вместе с тем следует отметить, что закон Дюлонга и Пти совершенно не применим при низких температурах. Вблизи абсолютного нуля ~ .

Некоторые вещества, например алмаз, имеют молярную теплоемкость >3R. (Алмаз 5,6*10³ Дж/(кг*К))

Квантовая теория теплоемкости Эйнштейна

В основе этой теории лежат следующие положения:

ü Энергия колебательного движения квантована;

ü Колебания частиц в решетке являются взаимосвязанными.

Вследствие взаимодействия между частицами кристалла возмущение какой-нибудь из них порождает бегущую волну. Достигнув стенки кристалла, она отражается и налагается на следующую бегущую волну. Возникают стоячие волны.

Кристалл представляет собой систему из N атомов, имеющую 3N степеней свободы, т.е. 3N типов колебаний с дискретными частотами .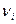

Подобно энергии электромагнитных волн, энергия тепловых акустических волн тоже квантована .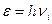

Квант звуковой энергии называется фононом. Квантовый характер тепловых волн проявляется при температурах ниже характеристической температуры Дебая .

,

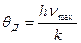где k – постоянная Больцмана;

h - постоянная Планка;

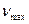- максимальная частота тепловых колебаний.

Сущность вытекает из следующих соображений:

На одну колебательную степень свободы приходится энергия равная kΤ. Когда она будет больше, чем h 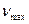, возбуждаются колебания любых частот и квантовый характер не проявляется.

Если kΤ < h 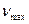, что имеет место при низких температурах, высокочастотные колебания не возбуждаются. Таким образом, температура Дебая является температурным рубежом, ниже которого проявляется квантовый характер тепловых волн.

Согласно теории Эйнштейна теплоемкость тела равна

.

При Т<< и С ~ (закон Дебая).

При Т >> C=3R (закон Дюлонга и Пти).

Понятие температуры Дебая хорошо описывает ход теплоемкости с температурой для кристаллов с простыми типами решеток. Для сложных соединений эта теория неприменима.

Тепловое расширение твердых тел

Рассмотрим более детально кривую потенциальной энергии. Эта кривая не является симметричной относительно r₀ . Это значение соответствует минимуму ε_пот. Здесь частицы неподвижны.

При повышении температуры до Т₁ среднее положение колеблющейся частицы не будет совпадать с r₀, а сдвинется вправо, достигнув значения r₁.

При возрастании температуры до Т₂ r₀ → r₂.

Таким образом, при возрастании температуры увеличивается расстояние между узлами кристаллической решетки, т.е. происходи тепловое расширение r₂ > r₁.

Для поликристаллов справедлива формула , где α - коэффициент линейного расширения.

Монокристаллы обладают анизотропией теплового расширения, т.е. коэффициент α для различных направлений внутри кристалла имеет разные значения. Так, например, выточенный из монокристалла шар, превращается в трехосный эллипсоид (с осями по трем взаимно перпендикулярным координатным осям).

Коэффициенты теплового расширения по трем кристаллографическим осям называются главными коэффициентами теплового расширения кристалла (α_1, α_2, α₃).

С понижением температуры α_1, α_2, α₃ тоже уменьшаются.

Пример: Фигура теплового расширения кальцита.

Решеточная теплопроводность

В твердых телах перенос тепла осуществляется за счет теплопроводности. Источниками передачи тепла служат колебания кристаллической решетки, и энергия тепловых колебаний передается от одного узла решетки к другому посредством установления волнового процесса.

Если концы твердого тела поддерживаются при разных температурах, то в образце возникает непрерывный поток теплоты. Количественно

,

где λ – коэффициент теплопроводности;

- градиент температуры;

dS – поперечное сечение.

Коэффициент теплопроводности λ численно равен количеству тепла, прошедшего через единицу площади в единицу времени.

Если h 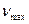≤ kΤ теплообмен возбуждает любые колебания и волны в кристалле, и квантовый характер теплообмена не заметен.

При h 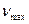≥ kΤ возбуждены колебания с низкими частотами, большие энергетические ступеньки не могут быть преодолены тепловыми толчками. Здесь следует учитывать квантовый характер тепловых волн.

По теории Дебая тепловое движение в кристаллах обеспечивается фононами.

Коэффициент теплопроводности выражается формулой

,

где С – теплоемкость единицы объема фононного газа;

l – средняя длина свободного пробега фонона4

υ_зв – скорость звука.

При высоких температурах (Т> ) λ ~ .

При Т→0^◦ К 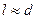, где d – размер образца.

Так как С ~ Т³, то λ ~ Т³.

Анизотропия сил связи приводит к анизотропии коэффициентов теплопроводности.

Все сказанное выше относится к так называемой решеточной теплопроводности, свойственной неметаллическим кристаллам.

В металлах кроме решеточной теплопроводности имеет место и перенос тепла при помощи электронов. При высоких температурах у чистых металлов решеточная теплопроводность составляет 1…2% от электронной. Этим объясняется высокая теплопроводность чистых металлов по сравнению с диэлектриками. Например, у алюминия λ = 0,54 ккам/(м*К⁴), а у кварца – на два порядка ниже.

Дата добавления: 2014-01-20