
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрические свойства твердых тел
|
|
|
|
Лекция № 16
Электропроводность металлов
Определения заряда электрона
Для понимания механизма электрических явлений необходимо знание природы элементарных носителей электрического заряда. Наименьшим количеством заряда, как известно, обладает электрон, поэтому он может быть назван атомом электрического заряда.
Наиболее убедительное доказательство атомной природы электрического заряда было получено в опытах Милликена и Иоффе. Идея опытов заключалась в следующем: если электрические заряды не имеют атомной природы, то заряд каждой частицы может изменяться непрерывно и принимать произвольные значения. В случае существования атомной природы электричества величина заряда должна изменяться скачкообразно, такими порциями, которые кратны элементарному заряду.
 Опыт Иоффе проведенный в 1912г. полностью подтвердил атомистический характер электричества.
Опыт Иоффе проведенный в 1912г. полностью подтвердил атомистический характер электричества.
В этом опыте отрицательно заряженная металлическая пылинка помещалась между обкладками конденсатора, напряженность поля в котором подбиралась такой, чтобы пылинка находилась в равновесии, т.е.
 .
.
 Затем пылинка освещалась ультрафиолетовым светом. Из-за фотоэффекта отрицательный заряд пылинки время от времени уменьшался и, для сохранения равновесия в конденсаторе, приходилось изменять напряженность электрического поля, т.е.
Затем пылинка освещалась ультрафиолетовым светом. Из-за фотоэффекта отрицательный заряд пылинки время от времени уменьшался и, для сохранения равновесия в конденсаторе, приходилось изменять напряженность электрического поля, т.е. 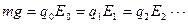 .
.
Откуда  :
: :
: =
=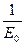 :
: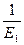 :
: .
.
Оказалось, что заряд пылинки может принимать лишь ряд дискретных значений.
Измерить величину элементарного электрического заряда впервые удалось Р.А. Милликену.
В пространство между пластинами конденсатора он вводил мельчайшие капельки масла. При разбрызгивании капельки электризовались, и их можно было установить неподвижно, подбирая величину и знак напряжения на конденсаторе.
Тогда  .
.
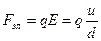 - сила, действующая на капельку со стороны электрического поля;
- сила, действующая на капельку со стороны электрического поля;
u – напряжение между пластинами конденсатора;
d – расстояние между ними.
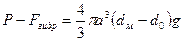 ,
,
Р – вес капли;
Fгидр – гидростатическая сила, действующая со стороны окружающего воздуха (сила Архимеда);
а – радиус капли;
dм – плотность масла;
d0 – плотность воздуха.
Записав вместо Fэл, Р и Fгидр их выражения, получим
 .
.
Таким образом, для определения заряда электрона достаточно найти радиус капли.
Для определения радиуса капли в микроскоп в отсутствии электрического поля наблюдалось прохождение ее между обкладками конденсатора, измерялось время прохождения, и определялась ее скорость.
Как известно из механики, на шар, движущийся ввязкой среде согласно закону Стокса, действует сила трения:
 ,
,
 - скорость шара;
- скорость шара;
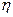 - коэффициент вязкости в среде.
- коэффициент вязкости в среде.
В состоянии равновесия  = движущей силе, т.е.
= движущей силе, т.е. 
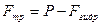
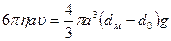
Откуда 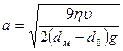 .
.
Таким образом, Милликен определил заряд капельки, полученный ею при распылении. Затем пространство между обкладками конденсатора облучалось рентгеновскими лучами. Происходила ионизация воздуха. Отдельные ионы, прилипая к капельке, изменяли ее заряд. Изменение заряда капельки каждый раз получалось кратным одной и той же величине. Эта величина и была принята за заряд электрона.
Тем самым была экспериментально доказана дискретность электрического заряда и измерено значение элементарного заряда, которое оказалось равным
 .
.
Природа носителей заряда в металлах
При раннем знакомстве с физикой мы узнали, что электрический ток в металлах – это движение электронов, и что ионы металла не принимают участия в переносе электрического заряда. Сейчас мы рассмотрим опытные доказательства этого.
Опыт Рикке
В основе опыта лежала проверка положения: если при электрическом токе имеет место движение ионов, то электрический ток в металлах должен обязательно сопровождаться переносом вещества металла. Для проверки этого Рикке в течение года пропускал электрический ток через три поставленных друг на друга цилиндра: медный, алюминиевый и медный. Несмотря на то, что общих заряд, прошедший через цилиндры, достигал огромного значения, около 3,5 млн кулонов, никакого проникновения металлов друг в друга обнаружено не было.
Следовательно, перенос заряда в металлах осуществляется не атомами, а какими-то другим частицами, входящими в состав металлов. Такими частицами могли быть электроны.
Наиболее убедительным доказательством электронной природы тока в металлах явились результаты опытов с инерцией электронов.
Если трамвай резко затормозить, то находящиеся внутри пассажиры будут двигаться по инерции вперед и скопятся на передней площадке. Аналогично, если резко затормозить движущийся кусок металла, то находящиеся в нем свободные заряды, двигаясь по инерции, будут скапливаться у его переднего конца и между концами проводника возникнет разность потенциалов.
 Существование подобных электроинерционных эффектов было установлено в 1913г. Мандельштамом Л.И. и Папалекси Н.Д. Катушка, соединенная с телефоном, приводилась в колебательное движение вокруг своей оси. Благодаря инерции свободных зарядов на концах катушки возникала переменная разность потенциалов, и телефон издавал звук.
Существование подобных электроинерционных эффектов было установлено в 1913г. Мандельштамом Л.И. и Папалекси Н.Д. Катушка, соединенная с телефоном, приводилась в колебательное движение вокруг своей оси. Благодаря инерции свободных зарядов на концах катушки возникала переменная разность потенциалов, и телефон издавал звук.
Количественные измерения относительной инертности носителей электрического тока в металлах были произведены в 1916г. Стюартом и Толмэном.
Схема опыта Стюарта и Толмэна изображена на рисунке.
Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы обмотки присоединялись к баллистическому гальванометру при помощи длинных гибких проводов, скручивающихся при вращении катушки. После раскручивания катушка резко тормозилась.
Двигаясь по инерции, свободные носители тока собираются в одном конце катушки и создают разность потенциалов, которая создает в цепи, замкнутой на гальванометр, ток силой і.
Обозначим заряд носителя электричества через е. Сила, действующая на этот заряд, равна

 ,
,
где Е – напряженность поля внутри проводника.
 ,
,
u – разность потенциалов на концах проводника;
L – длина провода в катушке.
Тогда  .
.
Импульс этой силы за время dt,, согласно закону сохранения импульса, равен
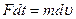 ,
,
где m – масса носителя электричества;
 - линейная скорость движения катушки или скорость движения в проводнике носителей электричества.
- линейная скорость движения катушки или скорость движения в проводнике носителей электричества.
Подставив вместо F ее значение, получим
 .
.
По закону Ома 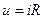 , где R – полное сопротивление цепи. Тогда
, где R – полное сопротивление цепи. Тогда
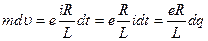 ,
,
где  - элементарное количество электричества, протекшее по проводнику за время
- элементарное количество электричества, протекшее по проводнику за время  .
.
Проинтегрировав это выражение по времени торможения катушки, получим
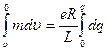 ,
,
где  - полный заряд, протекший через баллистический гальванометр (измеряется по отбросу последнего).
- полный заряд, протекший через баллистический гальванометр (измеряется по отбросу последнего).
После интегрирования
 .
.
Измеряя заряд  баллистическим гальванометром, и зная другие легко определяемые величины
баллистическим гальванометром, и зная другие легко определяемые величины  , можно найти отношение
, можно найти отношение  .
.
В результате опытов Стюарта и Толмэна, проведенных с различными веществами, было установлено, что величина  для всех веществ одинакова и равна
для всех веществ одинакова и равна  Кулон/кг.
Кулон/кг.
Незадолго до этого Милликен определил величину элементарного электрического заряда. Зная эту величину можно найти массу носителей электрического заряда. Она оказалась порядка 10-30 кг, что в 2000 раз меньше массы самого легкого атома – водорода ( ).
).
Полученные значения  и
и  оказались близки по своим значениям к аналогичным значениям, полученным для электронов другими методами (например, по отклонению электронов в электрических и магнитных полях).
оказались близки по своим значениям к аналогичным значениям, полученным для электронов другими методами (например, по отклонению электронов в электрических и магнитных полях).
Таким образом, было установлено, что носителями электрического тока в металлах являются свободные электроны.
Элементарная классическая теория электропроводности металлов
Исходя из представлений о свободных электронах, Друде разработал классическую теорию электропроводности металлов, которая затем была усовершенствована Лоренцем.
Согласно этой теории в металлах кроме отрицательных зарядов должны существовать и положительные заряды.
Эти положительные заряды металла представляют собой ионы, образующие кристаллическую решетку металла.
Электроны проводимости, вследствие теплового движения, хаотически перемещаясь, испытывают соударения с ионами решетки. При наложении внешнего поля электроны совершают упорядоченное движение, противоположное внешнему полю. Это и есть электрический ток.
В теории Друде-Лоренца предполагается, что движение электронов подчиняется законам классической механики Ньютона. Взаимодействием электронов между собой в этой теории пренебрегают, а взаимодействие электронов с положительными ионами сводят только к соударениям. Иными словами, электроны проводимости в металлах рассматриваются как «электронный газ», подобный идеальному газу, подчиняющемуся законам статистики Максвелла – Больцмана.
Согласно закону распределения энергии по степеням свободы, средняя энергия хаотического движения электронов в металле равна
 ,
,
где  - средняя квадратическая скорость электронов;
- средняя квадратическая скорость электронов;
 - масса электрона.
- масса электрона.
Отсюда 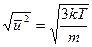 .
.
Обозначив через 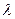 среднюю длину свободного пробега электронов в металле, можно найти время свободного пробега электронов
среднюю длину свободного пробега электронов в металле, можно найти время свободного пробега электронов  :
:
 ,
,
где  - средняя скорость движения электронов в металле (величина ее близка к
- средняя скорость движения электронов в металле (величина ее близка к  .
.
При включении поля на хаотическое тепловое движение электронов накладывается их упорядоченное движение с некоторой средней скоростью  .
.
Величину этой скорости можно найти из формулы, связывающей плотность тока  с числом носителей в единице объема
с числом носителей в единице объема  , их зарядом
, их зарядом 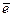 и средней скоростью
и средней скоростью  :
:  .
.
Скорость упорядоченного движения зарядов во много раз меньше средней скорости теплового движения, поэтому в дальнейших расчетах модуль результирующей скорости  можно заменить модулем скорости теплового движения
можно заменить модулем скорости теплового движения  .
.
Закон Ома в электронной теории металлов
Чтобы объяснить закон Ома с точки зрения электронной теории металлов и упростить расчеты, предположим, что при каждом соударении электрон передает решетке накопленную энергию полностью и поэтому, после соударения начинает движение без начальной скорости. Предположим так же, что при прохождении тока через проводник напряженность поля, создаваемого этим током, не изменяется.
На каждый электрон при движении действует сила  . Под действием этой силы электрон приобретает ускорение
. Под действием этой силы электрон приобретает ускорение  .
.
Скорость электрона к концу свободного пробега равна
 (аналог
(аналог 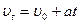 ,
,  ,
,  ).
).
Так как электрон между соударениями движется равноускоренно, то среднее значение его скорости равно половине максимального значения
 .
.
Подставив в эту формулу вместо  его выражение, получим
его выражение, получим
 .
.
И, наконец, подставив найденное значение скорости  в формулу для плотности тока, получим
в формулу для плотности тока, получим  .
.
Как следует из этой формулы, плотность тока пропорциональна напряженности поля, а это, как знаем, выражается законом Ома
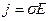 .
.
 - удельная проводимость материала проводника или коэффициент электропроводности.
- удельная проводимость материала проводника или коэффициент электропроводности.
Следовательно,  .
.
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость проводников, были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами, помещающимися в узлах кристаллической решетки металла.
Закон Джоуля-Ленца в электронной теории металлов
К концу свободного пробега электронов их кинетическая энергия равна
 .
.
Подставим вместо  ее значение. Тогда
ее значение. Тогда
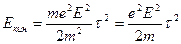 .
.
Заменив  его выражением, получим
его выражением, получим

 .
.
Столкнувшись с ионом, электрон полностью теряет приобретенную им за время пробега скорость, т.е. передает свою энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющейся в его нагревании.
Каждый электрон при своем движении претерпевает за секунду в среднем число соударений  .
.
 .
.
В единице объема за 1 секунду выделяется тепло
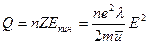 ,
,
 - число электронов в единице объема проводника.
- число электронов в единице объема проводника.
Т.к.  - удельная мощность тока, а в нашем случае
- удельная мощность тока, а в нашем случае 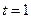 и
и  , то в формуле
, то в формуле  можно заменить на
можно заменить на  . Тогда
. Тогда

 .
.
Обозначим  через
через  , тогда
, тогда  .
.
Это и есть закон Джоуля-Ленца в дифференциальной форме.
Закон Видемана-Франца
Из опыта известно, что металлы, обладающие более высокой электропроводностью, имеют и лучшую теплопроводность. Видеман и Франц в 1853г. становил закон, согласно которому отношение коэффициента теплопроводности 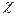 к коэффициенту электропроводности
к коэффициенту электропроводности  для всех металлов одинаково и увеличивается пропорционально абсолютной температуре.
для всех металлов одинаково и увеличивается пропорционально абсолютной температуре.
Электроны проводимости, перемещаясь в металле, переносят с собой не только электрический заряд, но и присущую им энергию беспорядочного теплового движения, т.е. осуществляют теплопередачу.
Рассматривая электроны как одноатомный газ, выражение для коэффициента теплопроводности можно записать как
 (см. тему «Механика: явления переноса»),
(см. тему «Механика: явления переноса»),
здесь  - плотность газа;
- плотность газа;
 - масса электрона;
- масса электрона;
 - число электронов в единице объема;
- число электронов в единице объема;
 - удельная теплоемкость при постоянном объеме;
- удельная теплоемкость при постоянном объеме;
 - средняя скорость теплового движения электронов;
- средняя скорость теплового движения электронов;
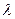 - длина свободного пробега электронов.
- длина свободного пробега электронов.
Как нам известно, удельная теплоемкость одноатомного газа равна
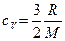 .
.
Величина универсальной газовой постоянной связана с постоянной Больцмана соотношением  .
.
С учетом этого  , а
, а  .
.
Разделив 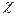 на выражение
на выражение  , полученное нами при выводе закона Ома, имеем
, полученное нами при выводе закона Ома, имеем
 .
.
Средняя энергия хаотического теплового движения электронов, как мы отмечали выше, равна  .
.
Заменив  через
через  получим
получим  - закон Видемана-Франца.
- закон Видемана-Франца.
Недостатки классической электронной теории проводимости металлов
Классическая электронная теория металлов смогла объяснить законы Ома, Джоуля-Ленца и дать качественное объяснение закона Видемана-Франца.
І. Вместе с тем согласие экспериментальных данных и теоретических расчетов для закона Видемана – Франца оказалось не очень хорошим. Лоренц уточнил расчеты, учтя распределение электронов по скоростям, и для отношения  получил значение
получил значение 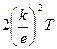 , которое согласуется с экспериментальными данными еще хуже. Это указывало на недостатки теории Друде-Лоренца.
, которое согласуется с экспериментальными данными еще хуже. Это указывало на недостатки теории Друде-Лоренца.
ІІ. Второе затруднение теории Друде-Лоренца возникло при сопоставлении с опытом килограмм-атомной теплоемкости одновалентного металла. Согласно теории, килограмм-атомная теплоемкость металла должна складываться из теплоемкости ионной кристаллической решетки, равной  , и теплоемкости электронного газа, равной
, и теплоемкости электронного газа, равной 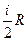
 .
.
У одновалентного металла 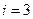 , следовательно
, следовательно  . Однако, опыт показывает, что килограмм- атомная теплоемкость металлов, как и других твердых тел, одинакова и равна
. Однако, опыт показывает, что килограмм- атомная теплоемкость металлов, как и других твердых тел, одинакова и равна  (закон Дюлонга и Пти).
(закон Дюлонга и Пти).
ІІІ. Третье затруднение классической электронной теории проводимости металлов заключается в невозможности правильно объяснить температурную зависимость электрического сопротивления.
Как мы уже знаем, электрическое сопротивление - это величина обратная коэффициенту электропроводности  , т.е.
, т.е. 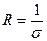 . В формуле для
. В формуле для  в знаменателе стоит величина средней скорости теплового движения электронов
в знаменателе стоит величина средней скорости теплового движения электронов 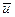 . Следовательно, для
. Следовательно, для  это значение будет в числителе, а так как
это значение будет в числителе, а так как 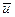 прямо пропорционально
прямо пропорционально 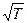 , то
, то  ~
~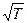 .
.
Однако, как показывает опыт,  ~
~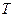 . Объяснение этим несоответствиям смогла дать лишь квантовая теория.
. Объяснение этим несоответствиям смогла дать лишь квантовая теория.
Несмотря на неспособность классической теории дать объяснение ряду явлений, она сохранила свое значение и до настоящего времени, потому что в случае малых концентраций свободных электронов (что имеет место в полупроводниках) она дает вполне удовлетворительные результаты. Вместе с тем, по сравнению с квантовой теорией, классическая теория обладает значительной простотой и наглядностью.
Элементы квантовой теории электропроводности
Функция распределения Ферми-Дирака и вырожденный электронный газ
Электрические, тепловые и оптические свойства металлов определяются состоянием свободных электронов и их распределением по энергиям. Такое распределение описывается квантовой статистикой Ферми-Дирака.
В основе ее лежат следующие положения:
1. все электроны в системе одинаковы (неразличимы);
2. состояние электрона определяется четырьмя квантовыми числами;
3. в системе не может быть больше одного электрона в данном квантовом состоянии.
Заполнение уровней электронами задается функцией Ферми:

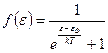
 (1).
(1).
Величина  называется уровнем Ферми.
называется уровнем Ферми.
Если в формуле (1)  , то
, то 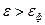 и
и  (это значит, что уровни выше уровня Ферми не заняты; вероятность заполнения равна нулю);
(это значит, что уровни выше уровня Ферми не заняты; вероятность заполнения равна нулю);
 Для
Для 
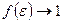 (уровни ниже уровня Ферми обязательно заняты; вероятность заполнения равна единице).
(уровни ниже уровня Ферми обязательно заняты; вероятность заполнения равна единице).
При любых температурах, если  , то
, то  ;
;
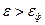 ,
, 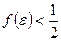 ;
;
 ,
, 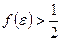 .
.
Чем выше температура, тем шире переходной участок от  до
до  .
.
Свободные электроны в металлах ведут себя подобно молекулам идеального газа. Поэтому их называют электронным газом. Свойства электронного газа принципиально отличаются от свойств идеального газа. Электронный газ в металле называется вырожденным газом. Основным признаком вырождения является независимость энергии его частиц от температуры. Электронный газ в металле остается вырожденным, пока любой из электронов не может обмениваться энергией с кристаллической решеткой,  (
( - энергия тепловых колебаний решетки), т.е. газ невырожден.
- энергия тепловых колебаний решетки), т.е. газ невырожден.
Температура, ниже которой газ переходит из невырожденного состояния в вырожденное называется температурой вырождения или температурой Ферми:
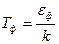 .
.
Таким образом, при  , т.е.
, т.е.  , электронный газ называют вырожденным;
, электронный газ называют вырожденным;  , т.е.
, т.е.  , электронный газ называют невырожденным.
, электронный газ называют невырожденным.
Теплоемкость электронного газа
Средняя энергия теплового движения, равная  , составляет при Т=300К
, составляет при Т=300К  . Такая энергия может возбудить только электроны, находящиеся на соседних с уровнем Ферми верхних уровнях. Основная масса электронов размещается на более глубоких уровнях и не будет поглощать энергию при нагревании. Таким образом, в процессе нагревания металла участвует незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газ в металлах. Формула теплоемкости электронного газа при постоянном объеме имеет вид:
. Такая энергия может возбудить только электроны, находящиеся на соседних с уровнем Ферми верхних уровнях. Основная масса электронов размещается на более глубоких уровнях и не будет поглощать энергию при нагревании. Таким образом, в процессе нагревания металла участвует незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газ в металлах. Формула теплоемкости электронного газа при постоянном объеме имеет вид:
 .
.
Обозначив 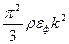 через
через  , получим
, получим 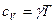 .
.
Имеем линейную зависимость  от температуры.
от температуры.
Измерения электронной теплоемкости (теплоемкость электронного газа) являются одним из прямых методов определения зонной структуры твердых тел.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1045; Нарушение авторских прав?; Мы поможем в написании вашей работы!