
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка гипотезы о значении математического ожидания генеральной совокупности
|
|
|
|
Пусть имеется генеральная совокупность распределенной по нормальному закону случайной величины 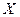 . Пусть генеральная дисперсия известна:
. Пусть генеральная дисперсия известна:  . Пусть извлечена
. Пусть извлечена 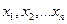 – выборочная совокупность объемом
– выборочная совокупность объемом 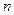 . Требуется по выборочной средней при заданном уровне значимости
. Требуется по выборочной средней при заданном уровне значимости 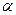 проверить нулевую гипотезу
проверить нулевую гипотезу  :
:  (о равенстве генеральной средней некоторому значению
(о равенстве генеральной средней некоторому значению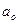 ).
).
Итак  :
:  ,
, 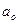 – некоторое число. Например,
– некоторое число. Например,  – размер детали (
– размер детали ( – распределена по нормальному закону) и
– распределена по нормальному закону) и 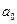 – проектный размер детали.
– проектный размер детали.
Предположим, что альтернативная гипотеза 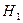 :
: 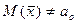 (это означает, что критическая область является двухсторонней.)
(это означает, что критическая область является двухсторонней.)
Выберем 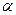 – уровень значимости гипотезы
– уровень значимости гипотезы  .
.
Построим статистический критерий  .
.
Найдем критическую область 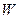 (для которой нулевая гипотеза
(для которой нулевая гипотеза  отвергается):
отвергается):
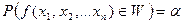 или
или  .
.
Очевидно, что вероятность попадания статистического критерия в область принятия гипотезы  есть
есть 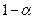 . Рассмотрим задачу нахождения вероятности того, что отклонение нормально распределенной величины
. Рассмотрим задачу нахождения вероятности того, что отклонение нормально распределенной величины 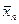 от параметра
от параметра 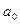 не превосходит по модулю некоторого числа
не превосходит по модулю некоторого числа 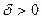 (т.е. определим границы области, где гипотеза
(т.е. определим границы области, где гипотеза  принемается):
принемается):
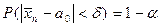 ,
,
тогда
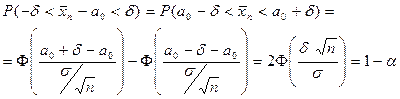
Следовательно
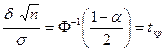 (находится из таблиц).
(находится из таблиц).
И, таким образом,  .
.
Тогда критическая область будет иметь вид:

Пример. Пусть 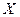 распределена по нормальному закону и
распределена по нормальному закону и 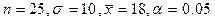 .
.
Необходимо проверить нулевую гипотезу  :
: 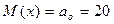 , при
, при 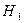 :
: 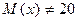 .
.
Так как 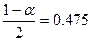 , то
, то 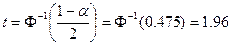 и тогда границы области допустимых значений определяются как:
и тогда границы области допустимых значений определяются как:
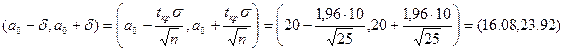
Ввиду того, что 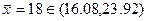 , т.е.
, т.е.  , то нулевая гипотеза
, то нулевая гипотеза принемается.
принемается.
Рассмотрим второй случай. Нулевая гипотеза  :
:  , альтернативная гипотеза
, альтернативная гипотеза 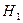 :
: 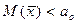 (это означает, что критическая область является левосторонней.) Далее по аналогии.
(это означает, что критическая область является левосторонней.) Далее по аналогии.
Выберем 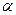 – уровень значимости гипотезы
– уровень значимости гипотезы  .
.
Построим статистический критерий  .
.
Найдем критическую область 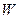 (для которой нулевая гипотеза
(для которой нулевая гипотеза  отвергается):
отвергается):
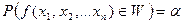 или
или  или
или 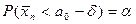
Очевидно, что вероятность попадания статистического критерия в область принятия гипотезы  есть
есть 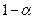 . Определим границы области, где гипотеза
. Определим границы области, где гипотеза  принимается:
принимается:
 ,
,
тогда
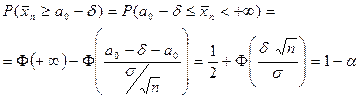
Таким образом, 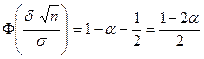 .
.
Следовательно
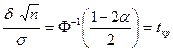 (находится из таблиц).
(находится из таблиц).
И, таким образом,  .
.
Тогда критическая область будет иметь вид:
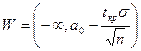 .
.
Т.е. если 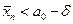 , то гипотеза
, то гипотеза  отвергается, если
отвергается, если , то гипотеза
, то гипотеза  принимаеся.
принимаеся.
Пример. Пусть 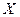 распределена по нормальному закону и
распределена по нормальному закону и 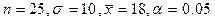 .
.
Необходимо проверить нулевую гипотезу  :
: 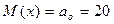 , при
, при 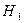 :
: 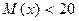 .
.
Так как 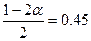 , то
, то 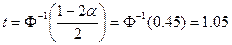 и тогда граница области допустимых значений определяется как:
и тогда граница области допустимых значений определяется как:
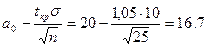
Ввиду того, что 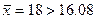 , т.е.
, т.е.  , то нулевая гипотеза
, то нулевая гипотеза принимается.
принимается.
Если в условиях примера 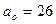 , то
, то 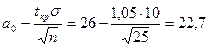 . В этом случае
. В этом случае 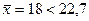 , т.е.
, т.е. 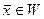 . Следовательно, нулевая гипотеза
. Следовательно, нулевая гипотеза отвергается в пользу
отвергается в пользу 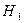 .
.
Рассмотрим третий случай. Нулевая гипотеза  :
:  , альтернативная гипотеза
, альтернативная гипотеза 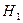 :
: 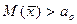 (это означает, что критическая область является правосторонней.) Далее по аналогии.
(это означает, что критическая область является правосторонней.) Далее по аналогии.
Выберем 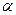 – уровень значимости гипотезы
– уровень значимости гипотезы  .
.
Построим статистический критерий  .
.
Найдем критическую область 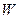 (для которой нулевая гипотеза
(для которой нулевая гипотеза  отвергается):
отвергается):
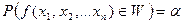 или
или  или
или 
Очевидно, что вероятность попадания статистического критерия в область принятия гипотезы  есть
есть 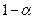 . Определим границы области, где гипотеза
. Определим границы области, где гипотеза  принемается:
принемается:
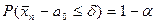 ,
,
тогда
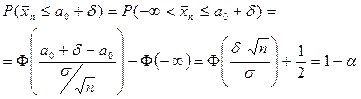
Таким образом, 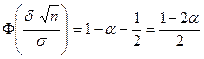 .
.
Следовательно
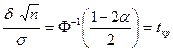 (находится из таблиц).
(находится из таблиц).
И, таким образом, 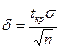 .
.
Тогда критическая область будет иметь вид:
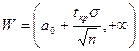 .
.
Т.е. если 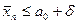 , то гипотеза
, то гипотеза  принемается, если
принемается, если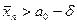 , то гипотеза
, то гипотеза  отвергается в пользу
отвергается в пользу 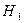 .
.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 866; Нарушение авторских прав?; Мы поможем в написании вашей работы!