
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка гипотезы о нормальном распределении генеральной совокупности по критериюК. Пирсона
|
|
|
|
Сущность проверки гипотезы о законе распределения эмпирических данных заключается в следующем. Имеется выборка эмпирических данных фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке степень согласованности эмпирических данных и выбранного закона распределения.
Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределений, т.е. при помощи специально подобранной случайной величины – критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Допустим, что в результате наблюдений получено эмпирическое распределение:
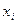
| 
| 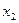
| … | 
|

| 
| 
| … | 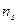
|
Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение, представленное в таблице с этой гипотезой.
Для проверки нулевой гипотезы о нормальном распределении генеральной совокупности существует несколько критериев согласия: хи-квадрат ( ) К. Пирсона, Колмогорова, Мизеса и др.
) К. Пирсона, Колмогорова, Мизеса и др.
Рассмотрим вопрос проверки согласованности распределений с использованием критерия  К. Пирсона.
К. Пирсона.
Предположим, что вычислены теоретические частоты: 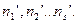
При уровне значимости 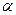 требуется проверить нулевую гипотезу: генеральная совокупность распределена по нормальному закону.
требуется проверить нулевую гипотезу: генеральная совокупность распределена по нормальному закону.
Обозначим через  среднее арифметическое квадратов разностей между эмпирическими и теоретическими частотами, взвешенное по обратным величинам теоретических частот:
среднее арифметическое квадратов разностей между эмпирическими и теоретическими частотами, взвешенное по обратным величинам теоретических частот:
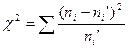 .
.
Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше будут различаться эмпирические и теоретические частоты, и тем меньше будет  . Уже отсюда видно, что
. Уже отсюда видно, что  в известной степени характеризует близость эмпирического и теоретического распределений. Очевидно, в разных опытах
в известной степени характеризует близость эмпирического и теоретического распределений. Очевидно, в разных опытах  будет принимать различные, наперед неизвестные значения, т.е.
будет принимать различные, наперед неизвестные значения, т.е.  является случайной величиной.
является случайной величиной.
Итак, в качестве критерия проверки нулевой гипотезы примем случайную величину  .
.
Дифференциальная функция этого распределения (для выборки достаточно большого объема) не зависит от проверяемого закона распределения (поэтому рассматриваемый критерий может применяться для проверки не только нормального, но и других законов), а зависит от параметра 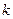 , называемого числом степеней свободы. При проверке гипотезы о нормальном распределении генеральной совокупности параметр
, называемого числом степеней свободы. При проверке гипотезы о нормальном распределении генеральной совокупности параметр 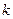 определяется формулой:
определяется формулой: 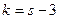 , где
, где  - число частичных интервалов, на которые разбиты данные наблюдений.
- число частичных интервалов, на которые разбиты данные наблюдений.
Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу  , чем двусторонний, построим правостороннюю критическую область, исходя из требования, что вероятность попадания критерия в эту область была бы равна принятому уровню значимости
, чем двусторонний, построим правостороннюю критическую область, исходя из требования, что вероятность попадания критерия в эту область была бы равна принятому уровню значимости 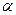 , т.е.:
, т.е.:
 .
.
Таким образом, правосторонняя критическая область определяется условием 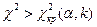 , а область принятия нулевой гипотезы – неравенством
, а область принятия нулевой гипотезы – неравенством  .
.
Следовательно, для того чтобы при заданном уровне значимости 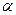 проверить нулевую гипотезу
проверить нулевую гипотезу : генеральная совокупность распределена нормально, необходимо вычислить значение критерия по данным выборки -
: генеральная совокупность распределена нормально, необходимо вычислить значение критерия по данным выборки - 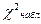 и сравнить его со значением
и сравнить его со значением 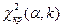 , определенным по таблицам.
, определенным по таблицам.
Если при этом 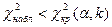 - то нет оснований отвергать нулевую гипотезу
- то нет оснований отвергать нулевую гипотезу  , если же
, если же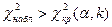 - то нулевая гипотеза
- то нулевая гипотеза  отвергается.
отвергается.
Замечание. На практике необходимо следить за тем, чтобы объем выборки был достаточно велик (в крайнем случае 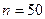 ) и чтобы каждая группа содержала не менее 5-8 значений признака (малочисленные группы следует объединить в одну, суммируя частоты).
) и чтобы каждая группа содержала не менее 5-8 значений признака (малочисленные группы следует объединить в одну, суммируя частоты).
Итак, для проверки нулевой гипотезы  о нормальном распределении генеральной совокупности следует:
о нормальном распределении генеральной совокупности следует:
1. вычислить теоретические частоты;
2. вычислить  ;
;
3. вычислить число степеней свободы 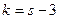 ;
;
4. выбрать уровень значимости 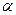 ;
;
5. найти по таблицам для найденных 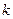 и
и 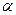 :
: 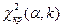
6. сравнить 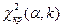 и
и  : если
: если 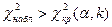 , то нулевую гипотезу о нормальном распределении генеральной совокупности отвергают; если же
, то нулевую гипотезу о нормальном распределении генеральной совокупности отвергают; если же 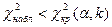 , то нулевую гипотезу принимают.
, то нулевую гипотезу принимают.
Пример. Проверить, согласуются ли данные выборки:
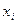
| |||||||||
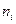
|
со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена эта выборка.
1. Теоретические частоты для данной выборки были получены ранее:
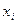
| |||||||||

|
2. Вычислим 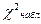 , для чего составим расчетную таблицу:
, для чего составим расчетную таблицу:

| 
| 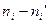
| 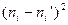
| 
|
| -1 -4 -8 -7 -1 | 0,07 0,38 0,78 0,49 1,07 1,32 0,09 | |||
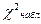 =9,2 =9,2
|
Сложив числа последнего столбца, найдем 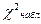 =9,2.
=9,2.
3. Вычислим число степеней свободы (учитывая, что число групп выборки  ):
):  .
.
4. Примем уровень значимости 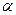 =0,01.
=0,01.
5. По таблице для  и
и 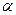 =0,01 найдем
=0,01 найдем 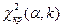 =16,8.
=16,8.
6. Сравнивая 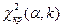 и
и  видим, что
видим, что 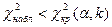 : 9,2<16,8.
: 9,2<16,8.
Следовательно, данные наблюдений согласуются с нулевой гипотезой о нормальном распределении генеральной совокупности.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2024; Нарушение авторских прав?; Мы поможем в написании вашей работы!