Дисперсия случайной дискретной величины

Закон распределения случайной величины характеризует ее полностью, но наиболее компактно можно выразить все существенные сведения о случайной величине, которыми мы располагаем, с помощью числовых параметров, получивших название числовых характеристик случайной величины. Оно соответствует тому значению случайной величины, около которого группируются все ее возможные значения.

Математическое ожидание случайной величины.

Числовые характеристики случайной величины

Сумма произведений всех возможных значений случайной величины на вероятности этих значений называется математическим ожиданием и обозначается символом М(Х), или т_Х, или m:

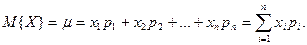(2)

Математическое ожидание случайной величины Х связано своеобразной зависимостью с ее средним арифметическим значением. При небольшом числе опытов среднее арифметическое случайно; при большом их числе оно приближается к постоянной величине – математическому ожиданию (центру распределения случайной величины).

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины С равно этой постоянной:

М{C} = C.

2. Постоянный множитель r можно выносить за знак математического ожидания:

M{rX} = rM{X}.

3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:

M{X ± Y} = M{X} ± M{Y}.

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

M{X Y} = M{X} × M{Y}.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания всегда равно нулю:

М(X - M{X}) = 0.

Часто требуется оценить рассеяние возможных значений случайной величины вокруг ее математического ожидания. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонений случайной величины от ее математического ожидания. Однако в силу свойства 5 М{X - m} = 0.

Для вычисления математического ожидания отклонения случайной величины берут отдельные ее отклонения по абсолютному значению, но это приводит при расчетах к большим затруднениям. Поэтому чаще всего вычисляют математическое ожидание квадратов отклонений.

Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется дисперсией случайной величины и обозначается символом s², или s²{Х}, или D{Х}, или s_х².

Слово «дисперсия» означает рассеяние. По определению

s² = М{(X - m)²}. (3)

Дата добавления: 2014-01-20