Способы определения вероятностей

Существуют два способа определения вероятности события.

1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле:

P(A)=m/n,

где m - число случаев, благоприятствующих наступлению события А; n - число всех равновозможных случаев из полной группы несов­местных событий.

Например, априори известно, что при одном выстреле в мишень равновероятно можно получить 0, 1, 2...10 очков. Какова вероят­ность того, что в результате одного выстрела будет получено 7 очков?

P(A) = m/n = 1/11= 0,091.

2. Статистический способ основан на предварительном прове­дении большого числа испытаний. При этом подсчитывают вероят­ность по формуле:

h (A) = k / L,

где k - число появления события А, называемое частостью А; L - общее число событий, наступивших в некоторой серии испытаний при определенном неизменном комплексе условий; h (A) - статисти­ческая вероятность события.

При большом числе испытаний значение частоты h (A) стабили­зируется и приближается к величине вероятности Р(A). Следует подчеркнуть, что статистическую вероятность события можно использовать в качестве значения вероятности только при большом числе испытаний.

В теории вероятностей существует большое количество математических соотношений, используемых на практике. Основные из них описывают сложение или умножение вероятностей.

Вероятность наступления ряда из m событий, принадлежащих к множеству несовместных N событий (N>m), равна сумме вероятностей этих событий:

P(A1+A2+...+Am) = P(A1)+P(A2)+...+P(Am).

Отсюда, в частности, следует, что сумма вероятностей собы­тий, образующих полную группу, равна 1; сумма вероятностей двух противоположных событий равна 0.

Например, известно, что экзаменационные оценки, полученные слушателями, распределились следующим образом: 4% слушателей по­лучили "2", 6 - "3", 60 - "4" и остальные 30% слушателей - "5". Какова вероятность, что указанный наугад слушатель этой группы получил отрицательную оценку?

P(2) = 4%/100% = 0,04.

Какова вероятность, что указанный наугад слушатель получил положительную оценку?

P(З,4,5) = P(3) + P(4) + P(5) =6%/100% + 60%/100% + 30%/100% = 0,06 + 0,6 + 0,3 = 0,96.

Вероятность одновременного наступления нескольких независи­мых событий равна произведению вероятностей этих событий:

P(C) = P(A1*A2*...*Ak) = P(A1)*P(A2)*...*P(Ak).

Два стрелка одновременно стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка (Р1) = 0,8, а для второго (Р2) = 0,6. Как найти вероятность того, что оба стрелка попадут в мишень?

Р = Р1* Р2 = 0,8 * 0,6 = 0,48.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности по­явления их совместного события:

P(C) = P(A+B) = P(A) + P(B) - P(A) * P(B)

Две поисковые группы участвуют в обнаружении преступника в лесном массиве. Вероятность обнаружения преступника первой груп­пой (Р1) = 0,8; второй группой (Р2) = 0,4. Какова вероятность того, что преступника обнаружит хотя бы одна группа?

Р = Р1 + Р2 - Р1 * Р2 = 0,8 + 0,4 - 0,32 = 0,88.

Математические соотношения теории вероятностей позволяют по вероятностям одних случайных событий находить вероятности других случайных событий, связанных с ними. Например, вероят­ность какого-либо события В, вычисленная в предположении, что перед этим наступило связанное с ним событие А, называется практические приложения соотношения условной вероятности можно проиллюстрировать следующими примерами.

При медицинском освидетельствовании лиц, претендующих на получение разрешения на вождение автомобиля, оказалось, что из N (общего числа претендентов) Na страдают дальтонизмом, Nb - женщины. Пусть А и В означают события, состоящие соответственно в том, что случайно выбранное лицо страдает дальтонизмом или яв­ляется женщиной. В частности, может оказаться необходимым найти вероятность того, что случайно выбранная женщина страдает даль­тонизмом, т.е. найти:

Р(А/В) = Р(АВ)/Р(В),

где: Р(А/В) - вероятность события А (дальтонизм) при условии, что произошло событие В (выбрана женщина); Р(AВ) - вероятность того, что женщина страдает дальтонизмом; Р(В) - вероятность то­го, что случайно выбранное лицо из N - женщина.

Так, при N = 240 и Nb = 30; Р(В) = Nb/N = 0,125. По дан­ным генетических исследований известно, что для женщин Р(АВ) = 0,0001. Таким образом, Р(А/В) = 0,0001/0,125 = 0,0008.

Следует отметить, что если Р(В/А) = Р(В) и Р(А/В) = Р(А), то события В и А взаимонезависимы.

Наряду со случайными событиями в теории вероятностей и ее применениях рассматриваются случайные величины. Представим себе, что при каждом наблюдении некоторая величина принимает какое-то значение в зависимости от случая. Например, количество звонков в дежурную часть по линии «02» за 1 час.

Случайные величины различаются как теми значениями, которые они способны принимать, так и вероятностями, с которыми эти значения принимаются. Например, вероятность того, что за промежуток времени t число вызовов патрульного наряда окажется равным k. Как показывают многочисленные наблюдения такая вероятность согласуется с формулой:

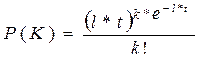
где l - некоторая положительная постоянная.

,а k! – факториал, причем n!= n (n - 1)(n - 2)...×3×2×1, пример: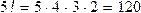

Эта формула получила название формулы Пуассона. Скорость молекулы газа также случайна и может принимать любые значения. Этих значений столько же, сколько положительных чисел. Как в этом случае задавать вероятности этих значений? Математики пошли по такому пути: стали определять не вероятность каждого из возможных значений, а вероятность того, что случайная величина x примет значение меньшее, чем заданное значение.

x: P { x < x } = F (x)

Функция F (x) наименование функции распределения случайной величины x. Из теоремы сложения легко вывести следующее равенство:

P { a £ x < b } = F(b) - F(a),

позволяющее по функции распределения определять вероятность выполнения указанного неравенства.

К более сложным соотношениям теории вероятностей относятся формулы Бернулли и Пуассона.

Формула Бернулли, описывающая вероятность того, что в N не­зависимых испытаниях, в каждом из которых вероятность появления события p (0 £ p £ 1), событие наступит k раз (безраз­лично - в какой последовательности), равна:

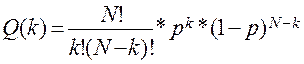
Например, состязаются два равносильных самбиста. Какова ве­роятность для одного из них выиграть две схватки из четырех?

Вероятность выигрыша p = 0,5, так как соревнуются два равных самбиста, и вероятность проигрыша 1-p = 0,5, тогда

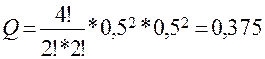
Дата добавления: 2014-01-20