Числовые характеристики вероятности

Наряду со случайными событиями в теории вероятностей и ее применениях рассматри­вают случайные величины. Представим себе, что при каждом наблюдении некоторая ве­личина принимает какое-то значение в зависи­мости от случая; например, число космиче­ских частиц, попадающих за данный проме­жуток времени на определенную площадку поверхности; число обрывов пряжи, изготовленной из хлопка определенного сорта и за­данного номера, при испытаниях на разрыв. Таких примеров можно привести сколько угодно.

Случайные величины различаются как теми значениями, которые они способны при­нимать, так и вероятностями, с которыми эти значения принимаются. Так, число вызовов от абонентов на телефонной станции за проме­жуток времени t может быть любым целым числом: О, 1, 2,.... Как показывают много­численные наблюдения, вероятность того, что число вызовов окажется равным k, согласует­ся с формулой 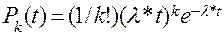, где 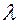не­которая положительная постоянная. Скорость молекулы газа также случайна и может принимать любые значения. Этих значений столько же, сколько положительных чисел. Как в этом случае задавать вероятности этих значений? Математики пошли по такому пути: стали определять не вероятность каждого из возможных значении, а вероят­ность того, что случайная величина 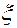, примет значение меньшее, чем заданное значение, 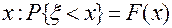. Функция F(x) получила на­именование функции распределения случай­ной величины 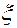;. Из теоремы сложения легко вывести следующее важное равенство: 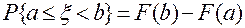, позволяющее по функ­ции распределения определять вероятность выполнения указанного неравенства.

В теории вероятностей и ее применениях важную роль играют числовые характеристики случайной величины - математическое ожидание и дисперсия.

Математическое ожидание. Во многих задачах случайная величина, рассматривается как возможный исход некоторого эксперимента, выражается вещественным числом. Например, число очков выбитых данным стрелком. Для всех этих случаев важной характеристикой случайной величины является ее математическое ожидание.

Определение. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятность.

Пусть, случайная величина Х может принимать только значения х₁, х₂,...х_n, вероятности которых соответственно равны p₁, p₂,...p₃. Тогда математическое ожидание М(Х) случайной величины определяется равенством

М(Х) = x₁p₁ + x₂p₂ +...... + x_np_n

Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Вероятностный смысл таков: математическое ожидание приближенно равно (тем точнее, чем больше испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания

1. Математическое ожидание постоянной величины равна самой постоянной.

М(С) = С

2. Постоянный множитель можно выносить за знак математического ожидания

М(СХ) = С * М(Х)

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

M(XY) = M(X)*M(Y)

Дисперсия. Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью не характеризует.

По этой причине, наряду с математическим ожиданием, вводят и другие числовые характеристики. Так, например, для того, чтобы оценить, как рассеяны возможные значения случайной величины вокруг математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией. Прежде чем перейти к определению и свойствам дисперсии, введем понятие отклонения случайной величины от ее математического ожидания.

Отклонением называют разность между случайной величиной и ее математическим ожиданием Х - М(Х), где Х - случайная величина, М(Х)

- ее математическое ожидание.

На практике часто требуется оценить рассеяние возможных значений случайной величины, вокруг его среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.

На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные отклонения случайной величины, а затем найти их среднее значение. Однако такой путь ничего не дает, т.к. среднее значение отклонения, т.е. M [ X - M(X)], для любой случайной величины равна нулю. Это объясняется тем, что одни возможные отклонения положительны, а другие отрицательные; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения послужили основанием целесообразности заменить отклонения их абсолютными значениями или их квадратами. Правда здесь приходится оперировать абсолютными величинами, что приводит иногда к затруднениями. Поэтому чаще всего вычисляют среднее значение квадрата отклонения, который и называют дисперсией.

Определение. Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

D(X) = M [ X - M(X) ]²

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю (С - постоянная величина)

D(C) = 0

2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат

D(CX) = C²D(X)

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин

D(X + Y) = D(X) + D(Y)

Среднее квадратичное отклонение

Для оценки рассеяния возможных значений случайной величины вокруг его среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение.

Определение. Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии

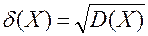
Т.е. среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность ее размерность совпадает с размерностью случайной величины. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если случайная величина выражается в метрах, то среднее квадратичное отклонение будет выражаться также в метрах, а дисперсия в квадратных метрах.

Дата добавления: 2014-01-20