Функция распределения

Каноническое распределение

Объект – равновесный идеальный газ из N частиц в объеме V в термостате с температурой Т. Полная энергия системы не постоянная, через стенки сосуда поступают и уходят микроскопические порции энергии. Поэтому разные микросостояния имеют отличающиеся энергии.

Получим распределение микросостояний по фазовому пространству.

Идеальный газ – любые подсистемы независимые, потенциальная энергия их взаимодействия друг с другом равна нулю. Систему делим на подсистемы 1 и 2. Соответствующие гамильтонианы связаны соотношением

.

Распределения для подсистем и для всей системы выражаются по теореме Лиувилля через гамильтонианы

,

,

.

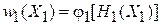По теореме об умножении вероятностей независимых событий распределения связаны

,

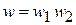тогда

.

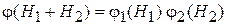Логарифмируем

,

берем бесконечно малое приращение – дифференциал

,

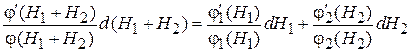где .

Учитываем, что 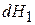и – независимые величины, тогда

.

Равенство выполняется при условии

,

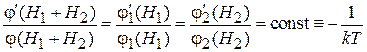где k – постоянная Больцмана. Далее будет показано, что T – температура.

Следовательно:

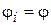– универсальная функция, удовлетворяющая уравнению:

.

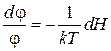Интегрируем

.

Полагаем

,

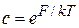как показано далее – свободная энергия системы. Получаем каноническое распределение

(2.15)

– вероятность обнаружения микросостояний в единице объема фазового пространства около точки X,

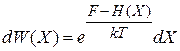(2.15а)

– вероятность обнаружения микросостояний в объеме dX фазового пространства около точкиX.

Статистический интеграл системы Z

Полагаем 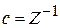, тогда

,

. (2.16)

Условие нормировки вероятности

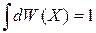
дает макрохарактеристику – статистический интеграл системы

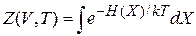. (2.17)

Статистический интеграл частицы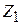

Для идеального газа из N тождественных частиц

,

,

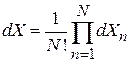где 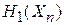– гамильтониан частицы n.

С учетом интеграл (2.17)

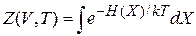
распадается на произведение N одинаковых интегралов. Получаем выражение стат. интеграла системы Z через стат. интеграл частицы Z ₁

, (2.18)

где статистический интеграл частицы

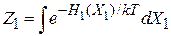, (2.19)

.

Для независимых видов движения частицы: поступательного, вращательного, колебательного и внутреннего

,

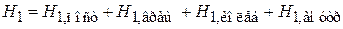тогда

. (2.20)

Для N частиц

. (2.21)

Далее получено

. (2.22)

Для двухатомной молекулы с моментом инерции J и частотой собственных колебаний w

,

. (2.23)

Физический смысл T

Общее начало термодинамики утверждает –если температуры систем одинаковые, то приведение систем в тепловой контакт не изменяет их макросостояний.

До контакта систем их функции распределения

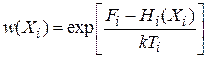. (2.16)

В момент контакта в силу независимости систем их общее распределение по теореме об умножении вероятностей

.

С течением времени гамильтонианы изменяются, их сумма сохраняется. Если температуры систем были одинаковыми, то распределение не должно меняться согласно общему началу термодинамики. Это возникает при . Следовательно, Т – температура по шкале Кельвина.

Дата добавления: 2014-01-20