Вариация числа микросостояний по объему

Микроканоническое распределение

Из (2.7)

,

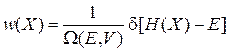и (2.10) получаем функцию распределения микросостояний по фазовому пространству

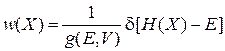. (2.10а)

Выразим термодинамические характеристики макросостояния через особенности распределения микросостояний по фазовому пространству.

Уравнение состояния газа описывает гиперповерхность 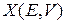в фазовом пространстве, на которой находятся микросостояния идеального газа с фиксированными значениями E, V, N. Интегрируем (2.9)

,

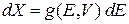и выражаем число микросостояний 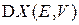внутри гиперповерхности через энергетическую плотность состояний

.

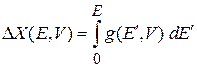Учитываем (2.8) и (2.10)

,

,

находим

.

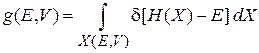Переставляем порядок интегрирований и получаем число микросостояний внутри гиперповерхности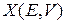

.

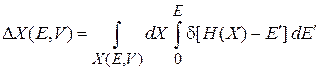Варьируем 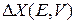по объему при постоянной энергии. От объема зависит гамильтониан, тогда

,

.

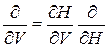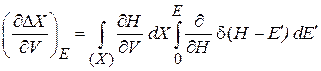Учитываем симметрию величин в аргументе дельта-функции и заменяем

,

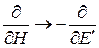получаем

.

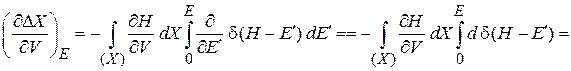
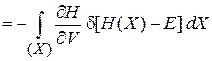При вычислении внутреннего интеграла учтено

,

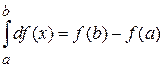на нижнем пределе 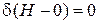, поскольку 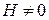. Используем (2.10а) в виде

,

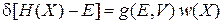тогда

.

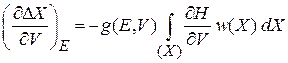По определению среднего для распределения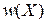

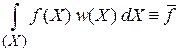
получаем

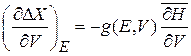. (2.11)

Внутренняя энергия U

Полная энергия описывается гамильтонианом системы H, и включает кинетическую и потенциальную энергию всех частиц системы. В общем случае эта энергия флуктуирует на микроскопическом уровне. При усреднении по фазовому ансамблю получаем макрохарактеристику – внутреннюю энергию

.

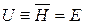Внутренняя энергия является полной энергией системы, усредненной по фазовому ансамблю.

Давление Р

Давление равно средней силе, действующей со стороны газа на единицу площади стенки сосуда. Давление выражаем через внутреннюю энергию изолированной системы с помощью первого начала термодинамики.

Первое начало термодинамики связывает количества тепла 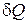, переданное газу, с изменением его внутренней энергии 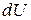и совершенной им работой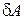

,

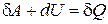где

.

Для изолированной системы

,

,

.

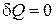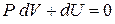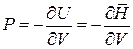Используем

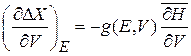. (2.11)

В результате давление выражается через статистические характеристики микросостояний

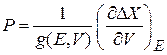. (2.12)

Энтропия S

Для равновесного обратимого изотермического процесса изменение энтропии пропорционально количеству полученного тепла

.

Вычисляем

,

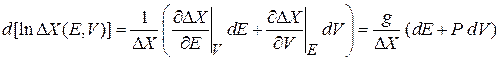где учтено (2.12) и

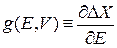. (2.9а)

Используем первое начало термодинамики для равновесного процесса

,

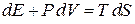получаем

.

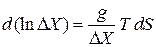Сравниваем сомножители бесконечно малой величины между собой

,

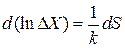и сомножители конечной величины между собой

,

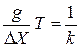где k – постоянная. В результате

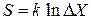, (2.13)

, (2.13а)

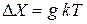. (2.14)

При рассмотрении конкретных систем и сравнении результатов с формулами термодинамики будет показано, что k – постоянная Больцмана, тогда kT – тепловая энергия.

Из (2.13) получаем – энтропия пропорциональна логарифму числа микросостояний.

Из (2.14) находим – число микросостояний равно произведению энергетической плотности состояний на тепловую энергию. Следовательно, микросостояния создаются за счет тепловой энергии.

Дата добавления: 2014-01-20