Следствия теоремы

Аналогично течет несжимаемая жидкость, сохраняя свою плотность. Теорему доказал французский математик Лиувилль в 1838 г. Теорема используется для получения функции распределения состояний по фазовому пространству.

Равновесный газ описывается стационарным гамильтонианом и постоянными термодинамическими параметрами. Макросостояние реализуется фазовым ансамблем микросостояний. Это множество точек с течением времени движется по фазовому пространству. Закон их перемещения описывает теорема Лиувилля – при движении точек фазового ансамбля плотность микросостояний в каждой точке фазового пространства постоянна и зависит от гамильтониана.

Теорема Лиувилля

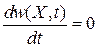. (2.5)

Жозеф Лиувилль (1809–1882)

Доказательство теоремы

Рассмотрим бесконечно малый объем фазового пространства в форме цилиндра с осью вдоль одной из обобщенных координат 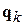. Основания цилиндра перпендикулярны оси, длина образующей .

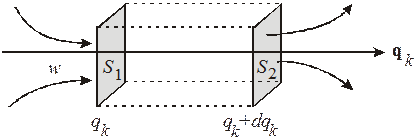
Микросостояния с плотностью 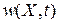входят в объем и выходят из него.

Для нахождения числа вошедших за 1с микросостояний представим микросостояние в виде жирной точки на рисунке. Число точек в единице объема равно w. Если все точки двигаются со скоростью , то за 1с через сечение пройдут состояния, которые первоначально заполняли цилиндр с длиной образующей, равной скорости. Умножаем объем цилиндра на плотность состояний, получаем число вошедших состояний

.

От точки к точке оси 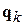меняется плотность состояний 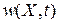и их скорость, тогда число состояний, выходящих через сечение равно

,

где использовано

.

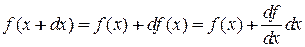Если с течением времени плотность 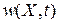изменяется, тогда в объеме появляются и исчезают состояния. За 1с в объеме 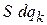появляется число состояний

.

Каждое состояние описывает реальную систему, поэтому число состояний сохраняется и выполняется уравнение баланса

«число появившихся состояний» =

= «число вошедших состояний» – «число вышедших состояний»:

.

Сокращаем подобные

.

Результат обобщаем на случай изменения координат фазового пространства

.

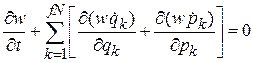Раскрываем круглые скобки

.

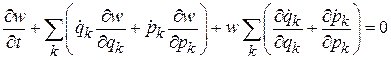Последняя скобка равна нулю согласно уравнениям Гамильтона (2.1)

, .

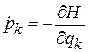Используем формулу для полной производной

,

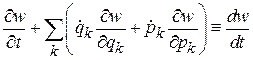и получаем теорему Лиувилля

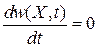
– полная производная по времени от плотности микросостояний равна нулю. Следовательно, плотность микросостояний фазового ансамбля не изменяется при его движении и зависит от гамильтониана.

Примечание: Полный дифференциал функции

Рассмотрим функцию . Если изменение функции при переходе между точками

,

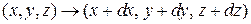находящимися в противоположенных вершинах параллелепипеда, не зависит от формы пути, то такая функция называется потенциальной. Выбираем путь, состоящий из трех участков, параллельных осям x, y и z. Тогда изменение складывается из изменений на каждом участке. Если участки бесконечно малые, то такое элементарное изменение функции называется полным дифференциалом

.

Деление результата на , дает полную производную

.

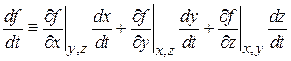Если функция не является потенциальной, то ее изменение зависит от формы пути. Элементарное изменение обозначается , формула полного дифференциала не применима.

Потенциальными функциями описываются гравитационное поле и электростатическое поле, магнитное поле описывается непотенциальными функциями. В термодинамике потенциальными функциями являются внутренняя и свободная энергии, непотенциальными функциями описываются работа и теплота.

А. Согласно теореме сохраняется число микросостояний в единице объема фазового пространства. Каждое микросостояние описывает реальный объект, и число микросостояний не зависит от времени. Тогда фазовый объем элемента ансамбля не изменяется с течением времени

,

изменяется лишь форма объема. Аналогично ведет себя несжимаемая жидкость. Учитываем

,

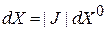где J – якобиан преобразования между начальными 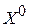и текущими X координатами, и получаем

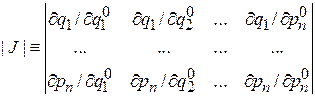= 1. (2.6)

Модуль якобиана, связывающего начальные и текущие фазовые координаты, равен единице. Результат используется при проверке выполнения теоремы Лиувилля для рассматриваемой системы.

Для одномерного движения частицы в плоскость 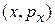получаем

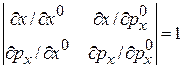. (2.6а)

Б. Для стационарной системы функция распределения не изменяется с течением времени согласно теореме Лиувилля, и может зависеть только от интегралов движения. Если система как целое неподвижна и не вращается, то функция распределения зависит от полной энергии, т. е. от гамильтониана:

. (2.6б)

В. Для равновесной изолированной системы

.

Система с равной вероятностью обнаруживается в любом из доступных микросостояний.

Г. Теорема не выполняется для диссипативных систем, т. е. при наличии трения и неупругих соударений. Диссипативная сила, действующая на тело со стороны среды, направлена против скорости движения тела относительно среды. Уравнения Гамильтона в виде (2.1) в этом случае не применимы.

Дата добавления: 2014-01-20