Микроканоническое распределение

ПРИМЕР

Одномерный гармонический осциллятор (двухатомная молекула с упругой связью, математический маятник, шарик на пружине, и т. д.) колеблется с частотой ω, имеет энергию E, и реализует микросостояние. Найти фазовую траекторию и проверить выполнение теоремы Лиувилля.

1. Энергия системы фиксирована, поэтому микросостояние в фазовом пространстве движется по гиперповерхности. Для одномерной системы из одной частицы координаты фазового пространства (x, p). Гамильтониан осциллятора приравниваем полной энергии

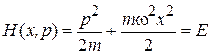
где

; ;

κ – коэффициент жесткости пружины.

2. Получаем уравнение фазовой траектории, по которой движется микросостояние:

.

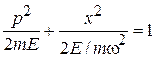Сравниваем с уравнением эллипса

,

находим полуоси

, .

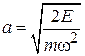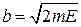Микросостояния отличаются друг от друга начальной фазой.

3. Находим число микросостояний (2.2а)

.

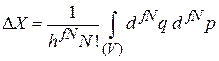При и 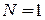интеграл равен площади эллипса

,

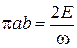тогда число микросостояний

, (П.2.4)

где 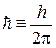. Следовательно, энергия осциллятора квантуется

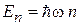, (П.2.4а)

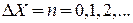где – квант энергии; – число микросостояний равно числу квантов энергии осциллятора.

На рисунке показан эквидистантный спектр энергиигармонического осциллятора. Горизонтальная линия – уровень энергии показывает возможное состояние осциллятора. Величина равна энергии одного кванта, или интервалу эквидистантного спектра. На уровне 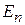осциллятор имеет n квантов энергии.

4. Для получения якобиана

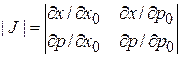
найдем функции

, ,

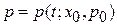где – начальная координата и начальный импульс при .

Используем уравнения Гамильтона (2.1)

, .

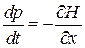Подставляем гамильтониан

,

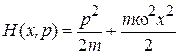получаем

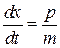– связь скорости с импульсом,

– 2-й закон Ньютона ,

где – коэффициент жесткости упругой силы F;

.

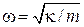Для решения системы двух уравнений дифференцируем первое уравнение

,

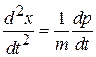подставляем второе и получаем уравнение гармонических колебаний

.

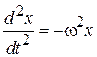Общее решение

,

.

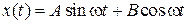Для нахождения свободных параметров A и B накладываем начальные условия

,

,

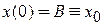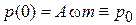получаем

, .

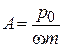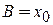Находим закон изменения координат микросостояния с течением времени

,

.

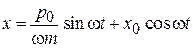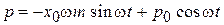Микросостояние перемещается по эллипсу по часовой стрелке с круговой частотой ω.

5. Вычисляем якобиан

.

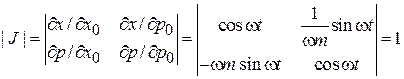Теорема Лиувилля выполняется.

Дата добавления: 2014-01-20